積分微分方程

積分微分方程是一類未知函式同時出現在積分和微分號下的方程。

定義

如果一個方程中，不僅出現未知函式的導數，而且未知函式或其導數還出現在積分號下面，這樣的方程就稱為積分微分方程。在擴散和輻射等物理問題中會碰到這種方程。

普朗特積分微分方程

【Prandtl integro-differential equation】

普朗特積分微分方程是有限翼展的飛機機翼的基本微分方程。

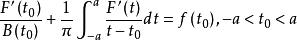積分微分方程

在推導普朗特積分方程時，假設機翼的每個元處於繞翼的平面平行流體中，得到的方程具有形式 ，其中，F是未知函式，B和f是給定函式，B(t)=cb(t)，f(t)=vω(t)，廣義積分理解為柯西主值的意義。

在方程中出現的量的物理意義如下：2a是機翼的翼展，它假定相對yz平面是對稱的且z軸方向與無窮遠處氣流方向相重合，b(x)代表對於橫坐標x的翼剖面翼弦，F(x)是該剖面周圍氣流的環流，c是常數，v是無窮氣流的速度，ω是依賴於剖面曲率和機翼扭曲的函式。

普朗特積分微分方程只是在非嚴格意義的假設下才能以封閉形式求解。在一般情況下，它可以轉化為弗雷德霍姆積分方程。