背景
PID控制是最早發展起來的控制策略之一，在PID 控制算法中，積分環節的引入其主要的目的是消除系統的穩態靜差、提高控制的精度。但是隨著積分環節的引入，相應也會出現一些問題，比如在過程的啟動、結束或較大幅度增減給定值時，短時間內系統輸出會有較大的偏差，由於PID運算的積分積累，可能導致控制量超過執行機構可能允許的最大動作範圍對應極限控制量，從而引起系統較大超調，甚至引起振盪，同時也增大了調節時間，這種現象在許多的生產過程中是絕對不允許的。正是在這種背景下產生了積分分離PID控制算法。積分分離PID控制算法根據實際情況引入或取消積分作用，使得控制系統的性能有了較大的改善。
基本原理
具有比例-積分-微分控制規律的控制器，稱PID控制器。其運動方程為：
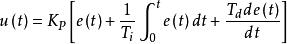積分分離PID控制
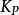積分分離PID控制式中，u(t)為進入受控對象的控制變數，e(t) =r (t) -y (t)為偏差信號，r (t)為設定的參考輸入值， 為比例係數，Ti為積分時間常數，Td為微分時間常數。
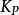積分分離PID控制比例環節是按比例反應系統的偏差信號e(t)，系統一旦出現了偏差,比例調節立即產生調節作用以減少偏差。比例作用大，可以加快調節，減少誤差，但是過大的比例 ，使系統的穩定性下降，甚至造成系統的不穩定。要有效消除靜差，需引入積分環節和微分環節。積分環節用於消除系統穩態誤差，提高無差度。輸出信號與偏差存在隨時間的增長而增強，直到偏差消除，輸出信號保持原輸出值不變,故能消除靜差。積分作用的強弱取決於積分時間常數Ti，Ti越小，積分作用就越強。反之則積分作用弱，但加入積分調節會使系統穩定性下降，動態過程變慢。而微分調節是指調節器的輸出與偏差對時間的微分成比例，微分調節器在溫度有變化“苗頭”時就有調節信號輸出，變化速度越快、輸出信號越強，故能加快調節速度，降低溫度波動幅度，改善系統的動態性能。在微分時間Td選擇合適情況下，可以減少超調，減少調節時間。微分作用對噪聲干擾有放大作用，因此過強的加微分調節，對系統抗干擾不利。
積分分離PID控制
具體實現
其基本原理為：被控量與設定值偏差較大時，取消積分作用，以避免由於積分作用使系統的穩定性降低，超調量增大，從而產生較大的振盪；當被控量接近給定值時，引入積分作用，以便消除靜態誤差，提高控制精度。其具體實現如下：
積分分離PID控制(1)根據實際情況，設定閾值 ；
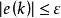積分分離PID控制(2)當 ，引入積分作用，採用PID控制，以消除靜態誤差，保證系統的控制精度；
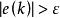積分分離PID控制(3)當 ，取消積分作用，採用PD控制，以避免由於積分作用使系統的超調增大，產生較大的振盪。
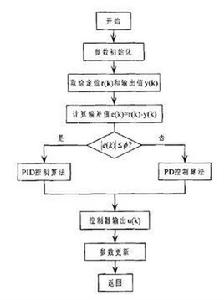
算法程式框圖
積分分離PID控制算法可表示為：
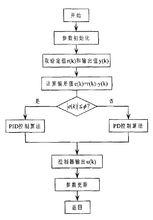圖1 積分分離PID控制算法程式框圖
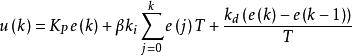積分分離PID控制式中，T為採樣時間，β項為積分項的開關係數。
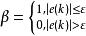積分分離PID控制上式中，ε為設定的閾值。
積分分離PID控制算法的程式框圖如圖1所示。當系統誤差較大時，取消積分環節，採用PD控制，避免由於積分累積引起系統較大的超調；當系統誤差較小時，引入積分環節，採用PID控制，以消除誤差，提高控制精度。
