簡介
有編號為⑴⑵⑶⑷⑸⑹⑺⑻⑼⑽⑾⑿的小球,其中有11個小球的重量相同,只有一個小球的重量和其它不一樣,使用一個無砝碼的天平稱3次,問怎樣稱能把該球找出來,並說出該球較其它球重還是輕。
動態稱法
此做法是最常見的處理手法,在各種答案中下表所列是其中的一種表述,對號入座即可:
| 第一次稱球情況 | 第二次稱球情況 | 第三次稱球情況 | 結論 | |||
| 首先 左⑴⑵⑶⑷:右⑸⑹⑺⑻ | 若左重 | 其次 左⑴⑸⑼:右⑵⑶⑹ | 若左重 | 最後 左⑷:右⑴ | 若平衡 | 則⑹輕 |
| 若右重 | 則⑴重 | |||||
| 若平衡 | 最後 左⑷⑻:右⑴⑵ | 若左重 | 則⑷重 | |||
| 若平衡 | 則⑺輕 | |||||
| 若右重 | 則⑻輕 | |||||
| 若右重 | 最後 左⑷⑻:右⑵⑸ | 若左重 | 則⑸輕 | |||
| 若平衡 | 則⑶重 | |||||
| 若右重 | 則⑵重 | |||||
| 若平衡 | 其次 左⑼⑾:右⑵⑽ | 若左重 | 最後 左⑼⑽:右⑴⑵ | 若左重 | 則⑼重 | |
| 若平衡 | 則⑾重 | |||||
| 若右重 | 則⑽輕 | |||||
| 若平衡 | 最後 左⑷:右⑿ | 若左重 | 則⑿輕 | |||
| 若右重 | 則⑿重 | |||||
| 若右重 | 最後 左⑼⑽:右⑴⑵ | 若左重 | 則⑽重 | |||
| 若平衡 | 則⑾輕 | |||||
| 若右重 | 則⑼輕 | |||||
| 若右重 | 其次 左⑴⑸⑼:右⑵⑶⑹ | 若左重 | 最後 左⑻⑼:右⑵⑸ | 若左重 | 則⑵輕 | |
| 若平衡 | 則⑶輕 | |||||
| 若右重 | 則⑸重 | |||||
| 若平衡 | 最後 左⑷⑻:右⑴⑵ | 若左重 | 則⑻重 | |||
| 若平衡 | 則⑺重 | |||||
| 若右重 | 則⑷輕 | |||||
| 若右重 | 最後 左⑷:右⑴ | 若左重 | 則⑴輕 | |||
| 若平衡 | 則⑹重 | |||||
判斷依據見後。
固定稱法
其實上面 動態稱法的方案就是專為本 固定稱法方案量身定做的。但本固定稱法的判斷並不依賴動態稱法,可獨立做出判斷。如圖所示,上表經整理後版面簡潔得多,判斷依據見後。
 稱球問題
稱球問題判斷依據
這是 動態稱法與 固定稱法共用的判斷依據。
首先我們可以在草稿紙上寫出所有嫌疑球號1、2、3、4、5、6、7、8、9、10、11、12,下列各情況相互獨立,互不影響。三次稱球,根據天平 依次呈現的狀態來對號入座。
若左重、左重、右重,為什麼判定是1號球重?
第一次左重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次左重,劃掉4、7、8,剩下1、2、3、5、6可疑
第一、二次均左重,劃掉2、3、5,剩下1、6可疑
第三次右重,劃掉6,僅剩1,可判定重
同理,若左輕、左輕、右輕,判定是1號球輕;
若左重、右重、右重,為什麼判定是2號球重?
第一次左重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次右重,劃掉4、7、8,剩下1、2、3、5、6可疑
第三次右重,劃掉3、6,剩下1、2、5可疑
第二、三次均右重,劃掉1、5,僅剩2,可判定重
同理,若左輕、右輕、右輕,判定是2號球輕;
若左重、右重、平衡,為什麼判定是3號球重?
第一次左重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次右重,劃掉4、7、8,剩下1、2、3、5、6可疑
第三次平衡,劃掉1、2、5,剩下3、6可疑
第一、二次分別左右重,劃掉6,僅剩3,可判定重
同理,若左輕、右輕、平衡,判定是3號球輕;
若左重、平衡、左重,為什麼判定是4號球重?
第一次左重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次平衡,劃掉1、2、3、5、6,剩下4、7、8可疑
第三次左重,劃掉7,剩下4、8可疑
第一、三次均左重,劃掉8,僅剩4,可判定重
同理,若左輕、平衡、左輕,判定是4號球輕;
若右重、左重、右重,為什麼判定是5號球重?
第一次右重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次左重,劃掉4、7、8,剩下1、2、3、5、6可疑
第三次右重,劃掉3、6,剩下1、2、5可疑
第一、三次均右重,劃掉1、2,僅剩5,可判定重
同理,若右輕、左輕、右輕,判定是5號球輕;
若右重、右重、平衡,為什麼判定是6號球重?
第一次右重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次右重,劃掉4、7、8,剩下1、2、3、5、6可疑
第三次平衡,劃掉1、2、5,剩下3、6可疑
第一、二次均右重,劃掉3,僅剩6,可判定重
同理,若右輕、右輕、平衡,判定是6號球輕;
若右重、平衡、平衡,為什麼判定是7號球重?
第一次右重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次平衡,劃掉1、2、3、5、6,剩下4、7、8可疑
第三次平衡,劃掉4、8,僅剩7,可判定重
同理,若右輕、平衡、平衡,判定是7號球輕;
若右重、平衡、左重,為什麼判定是8號球重?
第一次右重,劃掉9、10、11、12,剩下1、2、3、4、5、6、7、8可疑
第二次平衡,劃掉1、2、3、5、6,剩下4、7、8可疑
第三次左重,劃掉7,剩下4、8可疑
第一、三次分別左右重,劃掉4,僅剩8,可判定重
同理,若右輕、平衡、左輕,判定是8號球輕;
若平衡、左重、左重,為什麼判定是9號球重?
第一次平衡,劃掉1、2、3、4、5、6、7、8,剩下9、10、11、12可疑
第二次左重,劃掉12,剩下9、10、11可疑
第三次左重,劃掉11,剩下9、10可疑
第二、三次均左重,劃掉10,僅剩9,可判定重
同理,若平衡、左輕、左輕,判定是9號球輕;
若平衡、右重、左重,為什麼判定是10號球重?
第一次平衡,劃掉1、2、3、4、5、6、7、8,剩下9、10、11、12可疑
第二次右重,劃掉12,剩下9、10、11可疑
第三次左重,劃掉11,剩下9、10可疑
第二、三次次分別左右重,劃掉9,僅剩10,可判定重
同理,若平衡、右輕、左輕,判定是10號球輕;
若平衡、左重、平衡,為什麼判定是11號球重?
第一次平衡,劃掉1、2、3、4、5、6、7、8,剩下9、10、11、12可疑
第二次左重,劃掉12,剩下9、10、11可疑
第三次平衡,劃掉9、10,僅剩11,可判定重
同理,若平衡、左輕、平衡,判定是11號球輕;
若平衡、平衡、右重,為什麼判定是12號球重?
第一次平衡,劃掉1、2、3、4、5、6、7、8,剩下9、10、11、12可疑
第二次平衡,劃掉9、10、11,僅剩12
第三次右重,可判定重
同理,若平衡、平衡、右輕,判定是12號球輕。
經此表述將會發現,其實根本無需背誦,只需記住圖中固定稱球方案,即可臨機做出判定。
數學表達
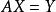 稱球問題
稱球問題將 固定稱法用矩陣方程寫出來思路會更清晰:
 稱球問題
稱球問題其中:
方程的含義為天平稱球的描述: 左盤總重量減 右盤總重量= 差值
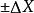 稱球問題
稱球問題首先:在12個球中,只有1個球與其它球重量不一樣,在邏輯上使用±1來代表重量差
 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題其次: 為3行12列係數矩陣,第 行第 列元素表示第 次第 號球的位置。1代表小球被放在左盤,-1代表小球被放在右盤,0代表小球不參與稱重
 稱球問題
稱球問題為12行1列矩陣,表示12個球的重量
 稱球問題
稱球問題為3行1列矩陣,表示3次稱球的結果。左盤重時得1;左右盤平衡時得0;右盤重時得-1
 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題最後:當 與 的第 列相等時,則第 球重;當 與 的第 列的負向量相等時,則第 球輕。
思路分析
 稱球問題
稱球問題根據方程的含義,上述 數學表達是明確的, 是方程的核心,現簡要闡述係數矩陣的一些特徵。
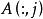 稱球問題
稱球問題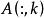 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題設 、 分別是係數矩陣 的第 列、第 列列向量,
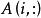 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題設 為 的第 行行向量,
 稱球問題
稱球問題只要同時滿足下列4個條件的 就是我們要尋找的係數矩陣。
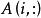 稱球問題
稱球問題1、 的所有分量求和=0,即任意一次稱球,天平兩端的球的個數相同;
 稱球問題
稱球問題 稱球問題
稱球問題2、 ,任意列向量非零(此處的 為零向量),即任意某個球至少被稱過1次;
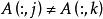 稱球問題
稱球問題3、 ,任意兩個列向量不相等;
 稱球問題
稱球問題4、 ,任意一個列向量與其它列向量的負向量不相等。
 稱球問題
稱球問題條件3、條件4是保證根據 做出無歧義判斷的關鍵。同時滿足這4個條件的係數矩陣有很多,但只要找到一個,就可寫出 數學表達方程式,也可以反演出 固定稱法,進而可反寫出 動態稱法。
縱觀全局,三個方案在表達方式上差別很大,但他們的本質卻是同一個答案。動態稱法直觀,但表達繁瑣,思路顯得凌亂;固定稱法簡潔明了,但理解上需要一定精力;經過解釋的數學表達思路明確,較容易抓住主線。
拓展
 稱球問題
稱球問題 稱球問題
稱球問題 稱球問題
稱球問題對於這一類稱球問題,歸納為使用天平 次,採取 固定稱法可在 個球中找出1個重量不一樣的球,並說出較其它球輕還是重。如果僅要求找出問題球,則可改為在 球中辨別出1個問題球。
