動態稱法
微軟的面試題:
分三組A1A2A3A4 B1B2B3B4 C1C2C34
第一步比較第一組和第二組 1.若A1A2A3A4=B1B2B3B4,問題球在C組裡;
第二步比較A1A2A3與C1C2C3
若A1A2A3=C1C2C3,則問題球為C4,比較C4與其他任意一球的輕重.
若A1A2A3>C1C2C3,則問題球在C1C2C3其中且為輕;
第三步比較C1C2:C1>C2,C2為問題球,C1<C2,C1為問題球,C1=C2,則C3為問題球;
若A1A2A3<C1C2C3;判斷方法和上面一樣,問題球為重球。
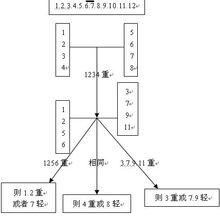 主線
主線2.若A1A2A3A4>B1B2B3B4則
第二步比較A1A2B1B2與A3B3C1C2
若A1A2B1B2=A3B3C1C2,則A4為重或B4為輕,A4>A1則問題球為A4,A4=A1則問題球為B4;
若A1A2B1B2<A3B3C1C2,則B1B2為輕球或A3為重球,第三步比較B1B2,哪個輕哪個就是問題球,
若一樣重,則A3為問題球且為重球;
若A1A2B1B2>A3B3C1C2,則A1A2中有一個重球或B3為輕;第三步比較A1A2,重的為問題球,
若一樣重則B3為問題輕球。
| 第一次稱球情況 | 第二次稱球情況 | 第三次稱球情況 | 結論 | |||
| 首先 左⑴⑵⑶⑷:右⑸⑹⑺⑻ | 若左重 | 其次 左⑴⑸⑼:右⑵⑶⑹ | 若左重 | 最後 左⑷:右⑴ | 若平衡 | 則⑹輕 |
| 若右重 | 則⑴重 | |||||
| 若平衡 | 最後 左⑷⑻:右⑴⑵ | 若左重 | 則⑷重 | |||
| 若平衡 | 則⑺輕 | |||||
| 若右重 | 則⑻輕 | |||||
| 若右重 | 最後 左⑷⑻:右⑵⑸ | 若左重 | 則⑸輕 | |||
| 若平衡 | 則⑶重 | |||||
| 若右重 | 則⑵重 | |||||
| 若平衡 | 其次 左⑼⑾:右⑵⑽ | 若左重 | 最後 左⑼⑽:右⑴⑵ | 若左重 | 則⑼重 | |
| 若平衡 | 則⑾重 | |||||
| 若右重 | 則⑽輕 | |||||
| 若平衡 | 最後 左⑷:右⑿ | 若左重 | 則⑿輕 | |||
| 若右重 | 則⑿重 | |||||
| 若右重 | 最後 左⑼⑽:右⑴⑵ | 若左重 | 則⑽重 | |||
| 若平衡 | 則⑾輕 | |||||
| 若右重 | 則⑼輕 | |||||
| 若右重 | 其次 左⑴⑸⑼:右⑵⑶⑹ | 若左重 | 最後 左⑻⑼:右⑵⑸ | 若左重 | 則⑵輕 | |
| 若平衡 | 則⑶輕 | |||||
| 若右重 | 則⑸重 | |||||
| 若平衡 | 最後 左⑷⑻:右⑴⑵ | 若左重 | 則⑻重 | |||
| 若平衡 | 則⑺重 | |||||
| 若右重 | 則⑷輕 | |||||
| 若右重 | 最後 左⑷:右⑴ | 若左重 | 則⑴輕 | |||
| 若平衡 | 則⑹重 | |||||
固定稱法
本方案與上述表格內的稱球方案是一致的:
第1次稱:左盤放置1、2、3、4號球, 右盤放置5、6、7、8號球
第2次稱:左盤放置1、5、9、11號球,右盤放置2、3、6、10號球
第3次稱:左盤放置4、8、9、10號球,右盤放置1、2、5、12號球
這樣稱就可以判斷是哪球重量不同,且說出該球較其它球是輕還是重,回答完畢。
 lanhenghui
lanhenghui按此做法,天平不管稱出什麼樣的結果,均可做出確定性的判斷985.so/cmeM
第1次、第2次、第3次天平依次呈現的狀態有:
若左重、左重、右重,判定1號球重;
若右重、右重、左重,判定1號球輕;
若左重、右重、右重,判定2號球重;
若右重、左重、左重,判定2號球輕;
若左重、右重、平衡,判定3號球重;
若右重、左重、平衡,判定3號球輕;
若左重、平衡、左重,判定4號球重;
若右重、平衡、右重,判定4號球輕;
若右重、左重、右重,判定5號球重;
若左重、右重、左重,判定5號球輕;
若右重、右重、平衡,判定6號球重;
若左重、左重、平衡,判定6號球輕;
若右重、平衡、平衡,判定7號球重;
若左重、平衡、平衡,判定7號球輕;
若右重、平衡、左重,判定8號球重;
若左重、平衡、右重,判定8號球輕;
若平衡、左重、左重,判定9號球重;
若平衡、右重、右重,判定9號球輕;
若平衡、右重、左重,判定10號球重;
若平衡、左重、右重,判定10號球輕;
若平衡、左重、平衡,判定11號球重;
若平衡、右重、平衡,判定11號球輕;
若平衡、平衡、右重,判定12號球重;
若平衡、平衡、左重,判定12號球輕。
矩陣方程
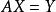 十二球
十二球將固定稱法用矩陣方程寫出來,思路會更清晰。
 十二球
十二球其中:
方程的含義為天平稱球的描述: 左盤總重量減 右盤總重量= 差值
首先:因為在12個球中,只有1個球與其它球重量不一樣,所以在邏輯上使用±1來代表重量差±△X
其次:A為3行12列係數矩陣,第i行第j列元素表示第i次第j號球的位置。1代表小球被放在左盤,-1代表小球被放在右盤,0代表小球不參與稱重
X為12行1列矩陣,表示12個球的重量
Y為3行1列矩陣,表示3次稱球的結果。左盤比右盤重時,用1表示;左右盤平衡時,用0表示;左盤比右盤輕時,用-1表示
然後:當Y與A的第j列相等時判定為第j球重;與A的第j列的負向量相等時判定為第j球輕。
最後:之所以能做出判斷,是由於A的任意列向量(或其負向量),均與A的其它列向量互不相等。
