社會統計分析
正文
統計描述 通過統計圖和統計表對社會研究中的調查資料作全面精確的分類和頻次研究，又稱分布研究。在全面研究的同時，對資料的特徵作簡化的研究。簡化研究包括集中趨勢和離散趨勢兩種：①集中趨勢研究資料的代表性數值。依據測量層次的不同，有眾值、中位值和均值 3種。眾值是具有頻次最多的觀察值，主要適用於定類變數的研究。中位值是觀察總數中位置居中的值，主要適用於定序變數的研究。均值的計算公式為
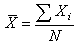
均值適用於定距以上的變數。3種集中值的選擇,雖然主要是根據測量層次來決定的，但還要根據數據分布的形狀，當分布嚴重偏態、非對稱時，一般採用中位值作為集中趨勢的度量。
②離散趨勢研究資料的分散程度。根據測量層次的不同,有異眾比例、極差和方差（標準差）3種。異眾比例是非眾值頻次在觀察總數中占的比例，主要適用於定類變數的研究。極差是觀察中最大值和最小值之差，主要適用於定序變數的研究。方差σ2的計算公式為
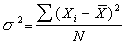
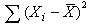為所有觀察值對均值的差值平方後的加總；N為觀察總數;方差的平方根為標準差
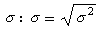。 方差適用於定距以上的變數。
集中趨勢和離散趨勢在對資料的簡化研究上是相互補充的。例如，均值說明資料的代表值是什麼，方差或標準差則說明資料圍繞均值的分散性如何。兩者的對應有：
眾 值凮異眾比例
中位值凮極差
均 值凮方差、標準差
除了上述兩類資料簡化研究的數值外，對於分布的特徵可作進一步細緻的研究。例如，通過偏態值研究分布是否對稱，通過峰態值研究分布的頂端是否尖陡。統計描述的分析，對於雙變數的調查資料，還可作相關性的研究，以確定變數間變化趨勢一致性的程度。
統計推論 根據局部的樣本資料推論總體的性質,以及通過樣本的描述性分析來估計總體特徵的一種方法。包括兩部分：①參數估計問題。根據樣本的觀察值，合理、科學地估計總體的特徵值，如均值、成數是什麼或在什麼範圍，並在給出估計範圍的同時，指示它可信的程度或置信度是多少。②假設檢驗問題。要求根據樣本資料對總體的假設，作出機率性的選擇。在接受總體假設時，要指出可能犯有納偽的錯誤；當拒絕總體假設時，又要指出可能犯有棄真的錯誤。任何一種判斷，無不帶有機率的性質，都是在非確定性預測中，求得最佳的抉擇。
