原理
磁場疊加原理是磁感應強度B所遵從的基本原理。它可以由磁場力的疊加原理導出。若空間一點有運動電荷或電流產生的磁感應強度B、永磁體的磁感應強度B、變化電場產生的磁感應強度B3,則該點的總磁感應強度為:
B=B+B+B
其中B1還可以是若干電流的磁場的疊加,B可以是若干永磁體磁場的疊加等。實驗也證明,任意電流在某點產生的磁場等於組成該電流的所有電流元在該點產生的磁場的矢量和,即
B=⨜B
疊加原理很重要,由畢奧—薩伐爾定律表示出dB後,再運用疊加原理B= ⨜dB,則任意恆定電流產生的磁場原則上就都可以求出了。
磁場
存在於載流導體、永久磁體、運動電荷或時變電場等周圍空間的,以磁感應強度表征的一種特殊形式的物質。磁場的物質性,可由它的如下許多特性顯示出來:磁場具有能量;磁場對運動電荷、載流導體有作用力;導線在磁場中運動或處在時變磁場中都將在導線中引起感應電動勢,發電機、變壓器就是根據這一原理製成的;在磁場的作用下,磁致伸縮材料會發生變形,呈現磁致伸縮現象;將載流導體置於磁場中,導體的橫向兩側將出現電位差,即產生霍耳效應;磁場可使載流導體或半導體的電阻發生變化,即產生磁致電阻效應,等等。描述磁場的基本物理量是磁感應強度B和重要的輔助量磁場強度H。
恆定磁場和時變磁場在空間某區域內,若各處的磁感應強度的量值和方向都不隨時間變化,該區域中的磁場稱恆定磁場,否則稱時變磁場。時變磁場總是和時變電場相互關聯,以電磁波的形式存在。研究某一區域中的時變磁場時,若電磁波的波長遠大於區域的線度尺寸,則可忽略位移電流對磁場的作用,這種時變磁場稱似穩磁場。大多數電力設備中的時變磁場可以認為是似穩磁場。
均勻磁場和非均勻磁場任何時刻,若空間某區域內各處的磁感應強度的量值和方向都相同,稱區域中的磁場為均勻磁場,否則稱非均勻磁場。
媒質的磁化位於磁場中的媒質將產生磁化效應。為巨觀描述媒質的磁化狀態及其對外磁場的影響,引入了磁場強度這一概念。磁感應強度和磁場強度的關係,常用磁化曲線表示。電機工程中,在許多場合下,只考慮鐵磁材料的磁化;非鐵磁材料的磁化很弱,一般不予考慮,即認為這種材料的磁導率和真空磁導率相同。
磁場的基本規律磁場具有如下的基本規律。
磁通量的連續性穿過任何閉合面的磁通量等於零(見磁通量)。
磁場強度的環路積分規律磁場強度沿閉合路徑的線積分,等於穿過以該閉合路徑為周界的曲面上的全電流(見磁場強度)。
磁場的能量密度線上性媒質中,單位體積內的磁場能量或磁場能量密度,等於(B·H)/2。
媒質分界面處磁場量滿足的條件在媒質1和媒質2的分界面上有:①媒質1、2的磁感應強度的法向分量BB連續,即B=B;②媒質1、2的磁場強度的切向分量H、H之差,等於分界面上的面電流密度Js(Js的方向垂直於H和H),即H-H=Js。不存在面電流時,H、H連續。
磁場力
磁場對磁體、電流或運動電荷的作用力稱為磁場力,簡稱磁力。電流在磁場中所受的力由安培定律確定。運動電荷在磁場中所受的力稱洛侖茲力。磁極在磁場中所受的力等於磁極強度和磁場強度的乘積。
磁感應強度
表征磁場強弱程度和磁場方向的物理量。又稱磁通密度。設磁場中某點有正電荷q,它的速度是v,磁場對它的作用力是F;改變速度v的方向但維持其量值不變,直到力的量值F為最大;定義該點的磁感應強度B的量值為B=F/qv,B的方向為F×v的方向。在國際單位制(SI)中,磁感應強度的單位是特[斯拉] (T);也有用高斯(Gs)作單位的。測量磁感應強度的常見方法,有基於感應電動勢效應的探測線圈法和基於霍耳效應的霍耳片法等。
磁感應線為了形象地描繪磁場,可畫出磁感應(強度)線的分布圖。在這種人為的有方向的磁感應線上,規定任一點的切線方向是該點的磁感應強度的方向。對於定性分析,所畫磁感應線的根數可隨意選定。如果還要求磁感應線能反映磁場強弱,可令垂直於磁場方向的單位截面積內穿過的磁感應線的根數,正比於該處的B值,從而磁感應線密度較大的地方,磁感應強度較大,即磁場較強。磁感應線通常是環繞電流的閉合曲線。圖示為載流螺線管的磁感應線分布圖。
磁場對運動電荷的作用力具有速度v的電荷q位於磁感應強度為B的位置時,電荷受到的力稱為洛倫茲力,按下式計算:
 磁場疊加原理
磁場疊加原理此式包含了B的定義。
磁場對載流導線的作用力長度是l的導線中通有電流I,當它置於磁感應強度是B的均勻磁場中時,導線受力F為:
 磁場疊加原理
磁場疊加原理當導線的方向與B的方向垂直時,力F的量值最大。此時,B、l和F三者互相垂直,可用左手定則描述為:伸開左手,讓磁感應線垂直進入手心,使合攏的四個手指指向電流的方向,則與四指相垂直的大拇指所指方向,就是載流導線所受磁場力的方向。
電流(沿閉合曲線)
畢奧-薩伐爾定律適用於計算一個穩定電流所產生的磁場。這電流是連續流過一條導線的電荷,電流量不隨時間而改變,電荷不會在任意位置累積或消失。採用國際單位制,用方程表示:
 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理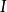 磁場疊加原理
磁場疊加原理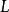 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理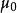 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理其中, 是源電流, 是積分路徑, 是源電流的微小線元素, 為電流元指向待求場點的單位向量, 為真空磁導率其值為 。
 磁場疊加原理
磁場疊加原理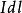 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理的方向垂直於 和 所確定的平面,當右手彎曲,四指從方向沿小於180度角轉向 時,伸直的大拇指所指的方向為 的方向, 即 、 、 三個矢量的方向符合右手定則。
積分通常圍繞閉合曲線,因為電流只能在閉合路徑周圍流動。無限長的電線(如電流SI單位定義中所使用的安培)是一個反例。
要套用公式,可以任意選擇要計算磁場的空間點(r)。保持該點固定,計算電流路徑上的線積分以找出該點處的總磁場。該法的套用隱含地依賴於磁場的疊加原理,即磁場是由電線的每個無窮小部分單獨產生的場的向量和的事實。
定律
在靜磁學中,畢奧-薩伐爾定律(英文:Biot-Savart Law)描述電流元在空間任意點P處所激發的磁場。
電流(沿閉合曲線)
畢奧-薩伐爾定律適用於計算一個穩定電流所產生的磁場。這電流是連續流過一條導線的電荷,電流量不隨時間而改變,電荷不會在任意位置累積或消失。採用國際單位制,用方程表示:
 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理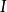 磁場疊加原理
磁場疊加原理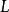 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理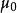 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理其中, 是源電流, 是積分路徑, 是源電流的微小線元素, 為電流元指向待求場點的單位向量, 為真空磁導率其值為 。
 磁場疊加原理
磁場疊加原理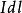 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理 磁場疊加原理
磁場疊加原理的方向垂直於 和 所確定的平面,當右手彎曲,四指從方向沿小於180度角轉向 時,伸直的大拇指所指的方向為 的方向, 即 、 、 三個矢量的方向符合右手定則。
積分通常圍繞閉合曲線,因為電流只能在閉合路徑周圍流動。無限長的電線(如電流SI單位定義中所使用的安培)是一個反例。
要套用公式,可以任意選擇要計算磁場的空間點(r)。保持該點固定,計算電流路徑上的線積分以找出該點處的總磁場。該法的套用隱含地依賴於磁場的疊加原理,即磁場是由電線的每個無窮小部分單獨產生的場的向量和的事實。
電流(整個導體體積)
當電流可以近似為穿過無限窄的電線時,上面給出的配方工作良好。 如果導體具有一定厚度,則適用於Biot-Savart定律(再次以SI為單位):
 磁場疊加原理
磁場疊加原理恆定均勻電流
在穩定的恆定電流I的特殊情況下,磁場B是
 磁場疊加原理
磁場疊加原理即電流可以從積分中取出。
