性質介紹
 磁圓二色性
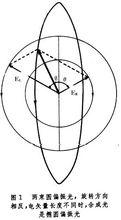
磁圓二色性介質對沿磁場方向傳播的一定頻率的左圓和右圓偏振光吸收率不同的性質。如果入射光是平面偏振光,
則磁圓二色性將使它在傳播過程中變為橢圓偏振光。在空間的固定點,它的電矢量末端沿橢圓形軌跡運動。
橢圓的長軸相對於入射光的偏振面旋轉一定角度,即磁致旋光現象。橢圓的短軸與長軸之比稱為橢圓率。
通常介質對左圓和右圓偏振光吸收率的差別,相對於吸收率本身來說是很小的,但現代儀器設備仍能精確測定它。磁圓二色性和磁致旋光同樣源於塞曼效應。
表示方法
 磁圓二色性
磁圓二色性磁圓二色性可以用對左圓和右圓偏振光的消光度之差:ΔA=A--A+,或吸收係數之差:Δk=k--k+=λΔA/4πllge來量度,式中λ是光波波長,
l是光在介質中的路程。
也可以用摩爾橢圓率【θ】M來衡量,這個量是參考圓二色性的摩爾橢圓率定義的:【θ】M=18 000θ/πcl,式中c是吸收光的分子的摩爾濃度;θ=πlΔk/λ,是以弧度表示的橢圓率;【θ】M則是以角度表示的。
貢獻原理
 磁圓二色性
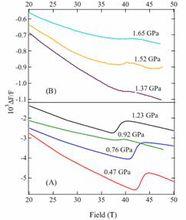
磁圓二色性磁圓二色性由A、B、C三項貢獻。A項來自基態和(或)激發態的塞曼分裂,該項隨頻率的變化具有吸收曲線對頻率微商的形式。
顯然,若基態和激發態都不是簡併的,則A項的貢獻為零。B項來自外加磁場引起的基態和(或)激發態與其他一些能態的混合。這種混合作用總是存在的。
這使磁致旋光和磁圓二色性成為一種對任何物質都存在的普遍效應。因為混合作用與被混合態的能級之差成反比,所以,若基態和激發態的近鄰都沒有可被混合的能態,則B項的貢獻很小。
C項來自加上磁場以後產生的基態能級分裂及其集居數的變化,由玻耳茲曼定律可知,集居數的變化與溫度有關。因此,C項是溫度的函式。當基態非簡併時,C項的貢獻為零。
B項或C項隨頻率的變化與吸收曲線類似。
由於磁圓二色性是消光度的差值,測量的靈敏度很高,用普通吸收方法不能分辨的塞曼分裂,可以用磁圓二色性譜來研究。
參數表征
在磁場不太強的情況下,A、B、C項可用一定參數(例如A1、B0、C0)來表征。
這些參數可以通過對磁圓二色性曲線的適當數學處理得到。
 磁圓二色性
磁圓二色性參數的數值和正負符號提供的信息,對於分子光譜的指認和分子電子結構(特別是前線分子軌道的性質)的研究很有用處。
例如A1≠0,表明基態或激發態是簡併的;
C0≠0,表明基態是簡併的;
A1=C0,則表明只有基態是簡併的;
A1≠0,C0=0,則可肯定激發態是簡併的。
B0較大,表示在基態或激發態的近鄰有可被混合的能級;
A項和C項的符號還可用來區別不同的躍遷。
若基態是非簡併的或者它的磁矩是已知的,則從A1可求出激發態的磁矩。根據電子結構特徵還可間接得到分子幾何構型(見分子的構型)的信息。
相關原理
與磁圓二色性譜密切相關的是磁致圓偏振螢光譜,它產生的機理與磁圓二色性譜相同,只不過它與自發輻射過程有關,而磁圓二色性譜則與光的吸收過程有關。