矩陣表示

簡介

在 V 上取一組基，把線性變換 ρ(g) 在此基下的矩陣記作 T(g)，則 g→ T(g) 是 G 到一般線性群 GL(n,K) 內的同態，它稱為 G 的矩陣表示。

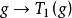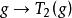等價矩陣表示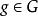

矩陣表示

矩陣表示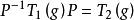

矩陣表示

矩陣表示

兩個矩陣表示和稱為等價的，如果有一可逆矩陣 P ，使得對一切，等式成立，所以對同一線性表示 ρ ，在 V 內取不同的基，所得到的矩陣表示是等價的。

表示論

[representation theory]

為了了解一個群的構造，我們常常研究它到某個具體的群內的同態，把這種同態稱為表示(representation)。最常見的具體的群有矩陣群（即矩陣組成的群）和置換群，所以常見的表示就是矩陣表示(matrix representation)和置換表示(permutation represenation)。

在矩陣表示的情況下，人們自然地把矩陣當成線性變換來對待，從而可以使用線性代數的豐富成果以得到深入的結論。於是把矩陣表示一般化為線性表示(linear representation)即群到線性變換群的同態。現在人們所說的表示論實際上是關於群的線性表示的理論。