概念
 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣矩陣是粒子物理標準模型的一個重要組成成份,它表征了頂類型和底類型夸克間通過 粒子弱相互作用的耦合強度。對二代夸克情形,它是由義大利物理學家卡比博在1963年首先給出的,通常被稱為卡比博矩陣或卡比博角。1973年日本物理學家小林誠和益川敏英把它推廣到三代夸克。三代矩陣含有相位,可以用來解釋弱相互作用中的電荷宇稱對稱性破缺( 破壞),也被經常用來解釋宇宙重子數不對稱。
基本原理
CKM矩陣元的測量
 CKM矩陣
CKM矩陣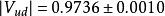 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣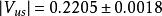 CKM矩陣
CKM矩陣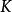 CKM矩陣
CKM矩陣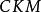 CKM矩陣
CKM矩陣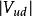 CKM矩陣
CKM矩陣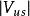 CKM矩陣
CKM矩陣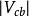 CKM矩陣
CKM矩陣絕大多數已知的 矩陣元都是用強子的半輕子道衰變方法測定的。例如, 是用原子核 衰變測定的,實驗選用強子效應儘量小的特定躍遷; 是從 介子半輕子道衰變測定的。儘管強子流的不確定性會影響 矩陣元測量的精確性,利用強作用對稱性、減少強子流不確定性影響,仍然能實現 和 的高精度測量。同樣,強作用對稱性在精確測定 中也起了重要作用。
 CKM矩陣
CKM矩陣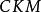 CKM矩陣
CKM矩陣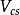 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣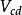 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣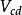 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣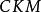 CKM矩陣
CKM矩陣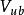 CKM矩陣
CKM矩陣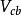 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣同 夸克有關的 矩陣元,如 可用 介子半輕子道衰變測定,而 是利用中微子與核的散射中的粲粒子產生加以測定的。 介子半輕子道衰變測定 ,精度受到形狀因子不確定性的限制。 介子半輕子道衰變主要用於研究粲夸克衰變振幅的絕對標度和檢驗強子流動力學。同 夸克有關的 矩陣元, 和 必須用 介子半輕子道衰變測定,而它們的絕對標度是理論上假設的。
CKM矩陣的表示
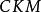 CKM矩陣
CKM矩陣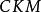 CKM矩陣
CKM矩陣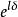 CKM矩陣
CKM矩陣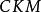 CKM矩陣
CKM矩陣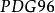 CKM矩陣
CKM矩陣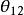 CKM矩陣
CKM矩陣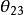 CKM矩陣
CKM矩陣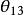 CKM矩陣
CKM矩陣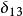 CKM矩陣
CKM矩陣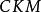 CKM矩陣
CKM矩陣在標準模型中, 矩陣元的數值同費米子質量一樣,不屬於理論預言的基本參量,而需要實驗測定。引入具有物理意義的么正條件和捨棄非物理的夸克相因子,理論得出:三代夸克的 矩陣只包含四個獨立的參量。這些參量的選擇有多種形式,但是,必須有一個相因子 。因此, 矩陣必須包含一個復元素。 採用一組角度 、 、 和 ,表示 矩陣,形式如下:
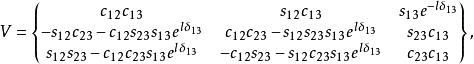 CKM矩陣
CKM矩陣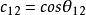 CKM矩陣
CKM矩陣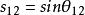 CKM矩陣
CKM矩陣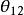 CKM矩陣
CKM矩陣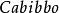 CKM矩陣
CKM矩陣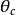 CKM矩陣
CKM矩陣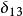 CKM矩陣
CKM矩陣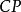 CKM矩陣
CKM矩陣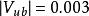 CKM矩陣
CKM矩陣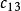 CKM矩陣
CKM矩陣其中 , 等等。 就是前面提到的 角 。因子 產生 破壞效應,在兩代夸克情況下這個因子消失。考慮到 非常之小和 非常接近於1,上式可以簡寫為:
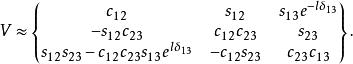 CKM矩陣
CKM矩陣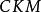 CKM矩陣
CKM矩陣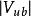 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣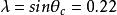 CKM矩陣
CKM矩陣矩陣元的數值依大小排列有層次之分,前面提到的 接近於零。1983年,有人建議將 矩陣按參數 作一展開,
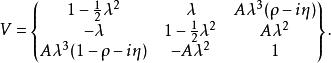 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣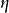 CKM矩陣
CKM矩陣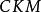 CKM矩陣
CKM矩陣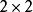 CKM矩陣
CKM矩陣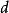 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣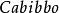 CKM矩陣
CKM矩陣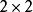 CKM矩陣
CKM矩陣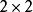 CKM矩陣
CKM矩陣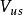 CKM矩陣
CKM矩陣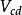 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣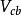 CKM矩陣
CKM矩陣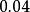 CKM矩陣
CKM矩陣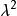 CKM矩陣
CKM矩陣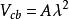 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣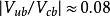 CKM矩陣
CKM矩陣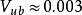 CKM矩陣
CKM矩陣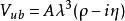 CKM矩陣
CKM矩陣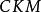 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣這裡,四個獨立的參量取為、、和。矩陣左上角的子陣就是和夸克轉動矩陣。實驗測量表明,這個子陣是近似的么正矩陣。展開式內子陣的非對角元素和等於,而對角元素等於加小修正量,以保持子陣的近似么正性。測量值約,取量級,因而寫作,其中是近似為的常數。實驗測量給出,或者,於是表達式中取。矩陣第三列元素同夸克相聯繫,它們的表示必須滿足么正性和正交性條件。這種近似的參量化方法在實驗研究中處理方便,因而得到廣泛套用。
CP破壞
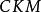 CKM矩陣
CKM矩陣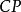 CKM矩陣
CKM矩陣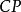 CKM矩陣
CKM矩陣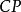 CKM矩陣
CKM矩陣三代夸克的矩陣包含一個相因子。在標準模型中,非零的相因子將導致破壞。這就是說,相應夸克躍遷振幅在正反粒子電荷和空間奇偶反演聯合變換下不具有不變性。破壞在理解粒子層次結構及其相互作用性質方面非常重要,而且在解釋世界以正物質(而非反物質)為主這一事實方面也是十分必要的。人們正以極大興趣尋找標準模型外破壞的來源。
 CKM矩陣
CKM矩陣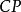 CKM矩陣
CKM矩陣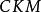 CKM矩陣
CKM矩陣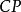 CKM矩陣
CKM矩陣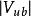 CKM矩陣
CKM矩陣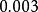 CKM矩陣
CKM矩陣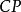 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣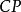 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣 CKM矩陣
CKM矩陣至今為止,僅在介子衰變中以千分之幾的微弱效應觀察到破壞現象。儘管觀察結果同標準模型預期一致,但是,實驗尚不能證實:矩陣是這種衰變發生破壞的可能解釋之一。事實上,標準模型以外的一些理論同樣可以解釋已有的衰變數據。值非常之小,但是,已測知其值不為零,約為。這個矩陣元不為零非常重要,否則標準模型將預期不存在破壞。此外,標準模型預期:介子衰變具有較大的破壞不對稱性。尋找介子衰變破壞的實驗計畫已在一些國家開始。
