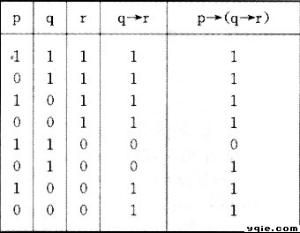
離散數學定義
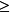真值表真值表是含n(n
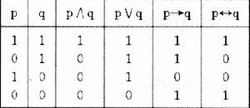
1)命題變項的命題公式 ，共有
組賦值將命題公式A在所有賦值之下取值的情況列成表，稱為A的真值表。
構造真值表步驟
真值表找出命題公式中所含的所有命題變項（若無下角標就按字典順序給出），列出所有的可能的賦值（）；
按從低到高的順序寫出各層次；
對應每個賦值，計算命題公式各層次的值，直到最後計算出命題公式的值。
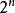真值表真值表的發展
4個公式的真值表發明真值表是用來在弗雷格、羅素等人開發的命題演算上工作的。它是在
1917年年由維根斯坦首次和1921年由 Emil Post 獨立發明的。真值表最初是作為一項邏輯矩陣的發現而產生的，十九世紀卓越的邏輯學家，美國人查爾士·山德爾斯·皮爾士以這項邏輯矩陣的發現為命題邏輯現代系統做出了重大貢獻。維根斯坦的邏輯哲學論使用它們把真值函式置於序列中。這個著作的廣泛影響導致了真值表的傳播。
真值表被用來計算真值泛函表達式的值(就是說是一個判定過程)。真值泛函表達式要么是原子(就是說是命題變數(或占位符)或命題函式 - 比如 Px)或建造自使用邏輯運算符(就是說 ∧ (AND)，∨ (OR)，¬ (NOT) - 例如 Fx & Gx)的原子公式。
真值表中的列標題展示了 (i) 命題函式與/或變數，和 (ii) 建造自這些命題函式或變數和運算符的真值泛函表達式。行展示對 (i) 和 (ii) 的 T 或 F 指派的每個可能的求值。換句話說，每行都是對 (i) 和 (ii) 的不同解釋。
實例
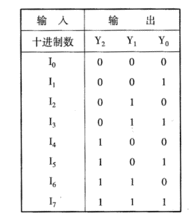bcd碼編碼器的真值表經典(就是說二值)邏輯的真值表限定於只有兩個真值是可能的布爾邏輯系統，它們
是真或假，通常在表中簡單的表示為 T 和 F。
舉例：用真值表方法回答：丁的話是否成立？為什麼？
甲：只有小王不上場，小李才上場。
乙：如果小王上場，則小李上場。
丙：小王上場，若且唯若小李不上場。
丁：甲、乙、丙的話都不對。
解答：列表：
真值表p q —p<-q p->q p<->—q
真 真 假 真 假
真 假 真 假 真
假 真 真 真 真
假 假 真 真 假
由表可知，丁的話不能成立，因為甲、乙、丙三人的話不可能同時為假。
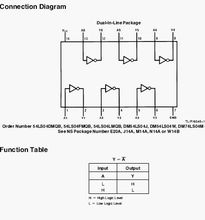74ls04引腳功能及真值表分析：以往的真值表解題，大都是要求判定兩個判斷是否等值或是否矛盾。近來
，一些真值表解題的要求有所改變，增加了試題考核的能力與難度層次。本例題就是一種類型。題目要求判定“丁的話是否成立”，實質上是要判定甲、乙、丙的話能否同假。
此類題目往往以自然語句出現，又規定了要用真值表方法解題，所以答題時的要領有以下幾個：一是把自然語句正確形式化，二是準確列出真值表，尤其是要小心求出判斷的真值，三是根據真值表作出判斷
