定義
兩個變數之間的皮爾遜相關係數定義為兩個變數之間的協方差和標準差的商：
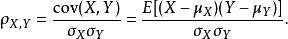皮爾遜積矩相關係數上式定義了 總體相關係數，常用希臘小寫字母 ρ(rho) 作為代表符號。估算樣本的協方差和標準差，可得到 樣本相關係數(樣本皮爾遜係數)，常用英文小寫字母 r 代表：
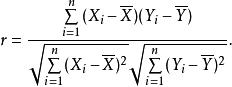皮爾遜積矩相關係數
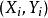皮爾遜積矩相關係數r 亦可由樣本點的標準分數均值估計，得到與上式等價的表達式：
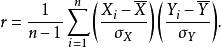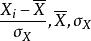皮爾遜積矩相關係數
皮爾遜積矩相關係數
皮爾遜積矩相關係數其中 分別是對 樣本的標準分數、樣本平均值和樣本標準差。
數學特性
總體和樣本皮爾遜係數的絕對值小於或等於1。如果樣本數據點精確的落在直線上（計算樣本皮爾遜係數的情況），或者雙變數分布完全在直線上（計算總體皮爾遜係數的情況），則相關係數等於1或-1。皮爾遜係數是對稱的：corr(X,Y)=corr(Y,X)。
皮爾遜相關係數有一個重要的數學特性是，因兩個變數的位置和尺度的變化並不會引起該係數的改變，即它該變化的不變數(由符號確定)。也就是說，我們如果把X移動到a+bX和把Y移動到c+dY，其中a、b、c和d是常數，並不會改變兩個變數的相關係數（該結論在總體和樣本皮爾遜相關係數中都成立）。我們發現更一般的線性變換則會改變相關係數：參見之後章節對該特性套用的介紹。
由於μ= E(X), σ= E[(X−E(X))] =E(X)−E(X)，Y也類似, 並且
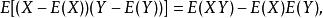皮爾遜積矩相關係數故相關係數也可以表示成
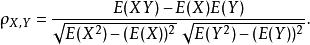皮爾遜積矩相關係數對於 樣本皮爾遜相關係數:
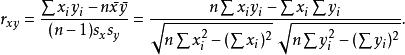皮爾遜積矩相關係數以上方程給出了計算樣本皮爾遜相關係數簡單的單流程算法，但是其依賴於涉及到的數據，有時它可能是數值不穩定的。
數據分布的敏感度
存在性
總體皮爾遜相關係數被定義成矩, 因此任意的雙變數機率分布是非零的， 也就是說總體協方差和邊緣總體方差是由定義的。 一些機率分布， 諸如柯西分布有未定義的方差，因此 Xor Y如果服從這種分布，ρ便是未定義的。 在實際套用中, 如果有數據被懷疑服從重尾分布, 這個條件就需要引起重視。 然而, 相關係數的存在性通常並需要太介意; 例如, 如果分布是有界的, ρ 便總是有意義的。
大樣本的特性
在雙變數常態分配的案例中， 只要邊緣均值和方差是已知的，總體相關係數描述的是便是聯合分布。 在其他的雙變數分布中，這個結論並不正確。 總之, 不論兩個隨機變數的聯合分布是不是正態的，相關係數在研究的它們之間的線性依賴性都是有幫助的。樣本相關係數是對兩個常態分配變數總體相關係數的最大似然估計並且是漸進無偏的 和有效的, 這也就是說如果數據是正態的並且樣本容量是中等的或大量的，就不可能構造出一個比樣本相關係數更準確的估計。對於非正態的數據, 樣本相關係數大致上是無偏的，但有可能是無效的。 只要樣本均值、方差和協方差是一致的（當大數定理可以套用的情況下），樣本相關係數是總體相關係數的一致估計。
穩健性
與其他常用的統計指標相似的, 樣本指標 r不是穩健的。因此如果由異常值，這個指標是有誤導性的。特別的, PMCC 既不是穩健分布的,也不是異常值穩健的(seeRobust statistics#Definition)。 對 X和 Y的散點圖的觀察可以很明顯的揭示出缺乏穩健性的情況,在這種情況下，採用的聯合的方法是比較明智的。 注意到，雖然大多數穩健的估計器從某種程度上說都是有統計依賴的, 它們總的來說，在總體相關係數的尺度上都是可辨的。
基於皮爾遜相關係數的統計推斷對數據分散式敏感的。 如果數據大致是常態分配的，可以使用精確檢驗和基於Fisher變換的漸進檢驗，但是它們可能由誤導性。 在一些情況下,自助採樣可以用來構造置信區間。 同時，重複抽樣可以套用在假設檢驗中。 這些非參數化的方法在某些情況下，如雙變數常態分配不能保證時，可能得出更有意義的結論。 然而，這些方法的標準形式依賴於數據的可交換性。這也就意味著被分析的數據時沒有順序的和組別的。因為這有可能會影響估計相關係數的特性。
分層分析是一種容許缺少雙變數正態性的方法，或者說是用來隔離相互關聯因素的關聯結果。 如果 W代表聚類成員或者其它需要被控制的因素，我們可以分離基於 W的數據, 然後我們可以再每個層里計算相關係數。 當我們控制變數 W，我們便能在層的等級上估計與所有相關係數相關的各自的相關係數。
強噪聲條件下
強噪聲條件下，提取相關係數兩個隨機變數之間的是平凡的，特別是在典型相關分析報告在退化的相關值的情況下，由於存在大量噪聲。一種概括的方法在其他地方給出。
維基相關條目
•相關
•史匹曼等級相關係數
•相關
•Disattenuation
•Maximal information coefficient
