原假設
“皮爾森卡方檢驗”的虛無假設（H）是：一個樣本中已發生事件的次數分配會遵守某個特定的理論分配。
在虛無假設的句子中，“事件”必須互斥，並且所有事件總機率等於1。或者說，每個事件是類別變數（英語：categorical variable）的一種類別或級別。
簡單的例子：常見的六面骰子，事件=丟骰子的結果（可能是1~6任一個）屬於類別變數，每一面都是此變數的一種（一個級別）結果，每種結果互斥（1不是2, 3, 4, 5, 6; 2不是1, 3, 4 ...），六面的機率總和等於1。
用途和步驟
“皮爾森卡方檢驗”可用於兩種情境的變項比較：適配度檢驗，和獨立性檢驗。
•“適配度檢驗”驗證一組觀察值的次數分配是否異於理論上的分配。
•“獨立性檢驗”驗證從兩個變數抽出的配對觀察值組是否互相獨立（例如：每次都從A國和B國各抽一個人，看他們的反應是否與國籍無關）。
不管哪個檢驗都包含三個步驟：
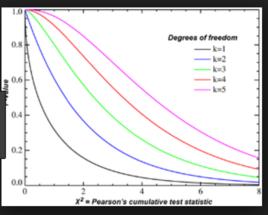
皮爾森卡方檢驗（1）計算卡方檢驗的統計值“ ”：把每一個觀察值和理論值的差做平方後、除以理論值、再加總。
皮爾森卡方檢驗（2）計算 統計值的自由度“df”。
皮爾森卡方檢驗（3）依據研究者設定的置信水準，查出自由度為df的卡方分配臨界值，比較它與第1步驟得出的 統計值，推論能否拒絕虛無假設。
適配度檢驗
適配度檢驗（英語：Goodness of Fit test）：測試樣本的機率分配與母體有多相似。
母體假設為離散型均勻分配
當理論上的母體分配為每個類別機率一致時，即應適用離散型均勻分配的計算方法。N個觀察值於理論上應均勻分配在所有的 m個欄位（類別）中，因此每個欄位（類別）的“理論次數”（或期望次數）為：
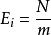皮爾森卡方檢驗，其中i=1,2,...,m.
皮爾森卡方檢驗其中，自由度df=m-1 。“m”是總共要計算離差平方的個數（每個類別計算一次觀察值與理論值的差，再平方）。“ -1”是因為對於計算 而言只有一個限制條件：觀察值的個數總和為N。
獨立性檢驗
在同一個個體（例如：同一個人）身上有兩個二元變數（X, Y），例如 X（男/女）和 Y（右撇子/左撇子），觀察兩個變數的相關性。 虛無假設是：兩個變數呈統計獨立性。
在本例中：性別與慣用手是獨立事件。
首先，每個觀察值（每個抽出的人）會被重新編排到一個叫做“列聯表”（英語：contingency table，又稱：條件次數表）的二維表格里。本例的列聯表是2×2的構造：
| 男 | 女 | 總計 | |
| 右 | 43 | 44 | 87 |
| 左 | 9 | 4 | 13 |
| 總計 | 52 | 48 | 100 |
如果列聯表共有 r 行 c 列，那么在獨立事件的假設下，每個欄位的“理論次數”（或期望次數）為：
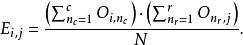皮爾森卡方檢驗其中 N是樣本大小（觀察值的個數，亦即2×2列聯表所有欄位的總和，本例：N = 100）。本例的各欄位期望值如下（括弧里的數字）：
| 男 | 女 | 總計 | |
| 右 | 43 (45.24) | 44 (41.76) | 87 |
| 左 | 9 (6.76) | 4 (6.24) | 13 |
| 總計 | 52 | 48 | 100 |
皮爾森卡方檢驗統計值的公式是：
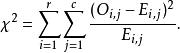皮爾森卡方檢驗 皮爾森卡方檢驗本例的統計值是：
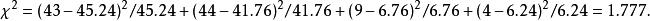皮爾森卡方檢驗自由度df=(r-1)(c-1)是這樣得出：雖然總共要計算 rc 個離差平方（每個欄位計算一次觀察值與理論值的差，再平方），但 X 變數有1個限制條件（樣本抽出後，男性的人數即固定），Y 變數也有1個限制條件（樣本抽出後，右撇子的人數即固定），所以可自由變動的欄位數只有 (r-1)(c-1).
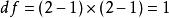皮爾森卡方檢驗在本例中.
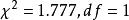皮爾森卡方檢驗在 的條件下，得出卡方分配右尾機率p=0.1825，無法拒絕虛無假設，亦即： 無法拒絕性別變數與慣用手變數互相獨立的假設。
限制
如果個別欄位的期望次數太低，會使機率分配無法近似於卡方分配。一般要求：自由度df>1時，期望次數小於5的欄位不多於總欄位的20%。
若自由度df=1，且若期望次數<10，則近似於卡方分配的假設不可信。此時可以將每個觀察值的離差減去0.5 之後再做平方，這便是葉氏連續性修正。
1.如果個別欄位的期望次數太低，會使機率分配無法近似於卡方分配。一般要求：自由度df>1時，期望次數小於5的欄位不多於總欄位的20%。
2.若自由度df=1，且若期望次數<10，則近似於卡方分配的假設不可信。此時可以將每個觀察值的離差減去0.5 之後再做平方，這便是葉氏連續性修正。
