簡介
畢渥數（Biot數）為傳熱學術語，記為 B i 。與傅立葉數（ Fo）、普朗特數（ Pr）、努塞爾數（ Nu）等無量綱數一樣都是傳熱學重要參量。
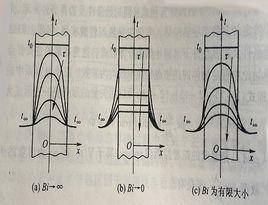
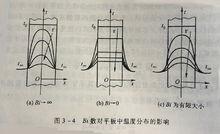Bi數對平板溫度分布的影響定義：表征固體內部單位導熱面積上的導熱熱阻與單位面積上的換熱熱阻（即外部熱阻）之比。
B i=δh/λ
其中，h為表面傳熱係數；λ為固體導熱係數；δ為特徵長度，通常用l表示。對於厚度為2δ平板l=δ，對於圓柱和球l=R。此外有些時候取l=V/A（V即體積，A為 換熱面積）。
Bi數提供了一個將固體中的溫差與表面和流體之間的溫差相比較的量。如果Bi<=0.1，物體最大與最小過餘溫度之差小於5%，對於一般工程計算，此時已經足夠精確的可以認為整個物體溫度均勻。這樣可以利用集中參數法研究問題。
Bi越小，表示內熱阻越小，外部熱阻越大。此時對於瞬態問題，採用集中參數法求解更為合適。
物理意義： Bi的大小反映了物體在非穩態導熱條件下，物體內溫度場的分布規律。或者認為是固體內部導熱熱阻與界面上換熱熱阻之比。
與Nu數的區別
努塞爾數Nu=hl/λ，表達式看起來與畢渥數相同，但二者意義有本質區別，Nu數表示壁面上流體無量綱溫度梯度（ λ為流體導熱係數），用於研究對流傳熱問題；而Bi數用於研究導熱問題，為固體內部導熱熱阻與界面上換熱熱阻之比。
關於Bi數在非穩態導熱問題的具體套用可以參考傳熱學相關資料。
其他說明
J.W.Biot(1774－1862)，法國物理學家。他的最大貢獻是對光的偏振現象的研究。他先於傅立葉（Fourier）研究了固體導熱問題，並已經認識到應當將表面的對流傳熱考慮到導熱問題中，但未能獲得分析解。
1804年，畢渥根據平壁導熱的實驗，發表學術論文，提出了導熱量正比於兩側溫差、反比於壁厚的概念。傅立葉正是在閱讀此篇文章後，在1807年提出求解偏微分方程的分離變數法和可以將解表示成一系列任意函式的概念。
此外BIOT可以指英屬印度洋領地（British Indian Ocean Territory，BIOT）。
