意義
對正常邊界表面來說，對流和傳導熱流是平行的，在簡單的情況下都垂直於平均流體的流動。
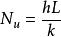努賽爾數式中，h是流體的對流換熱係數，L是特徵長度，k是流體的熱傳導率。
需要注意的是：
特徵長度的選擇應在邊界層的生長方向（或厚度）上；特徵長度的一些示例是：（外部）橫流（垂直於氣缸軸線）的氣缸的外徑，經受自然對流的垂直板的長度或球體的直徑。 對於複雜的形狀，長度可以定義為流體的體積除以表面積。
流體的熱導率通常（但不總是）評判膜溫度，這對於工程目的可以計算為散裝流體溫度和壁表面溫度的平均值。
與上面給出的定義相反，稱為平均努賽爾數。通過將長度作為距離表面邊界到當地感興趣點的距離來定義局部努塞爾數。
推導過程
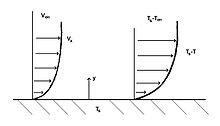熱邊界理解對流邊界層對於理解流過表面其的流體之間的對流傳熱是非常必要的。 如果無流體溫度和表面溫度不同，則會發生熱邊界層。 由於由該溫度差引起的能量交換，存在溫度差值。
傳熱率可以寫成：
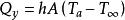努賽爾數又因為表面的熱是通過傳導而來的，所以：
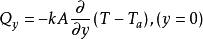努賽爾數由於上述兩式相等，因此：
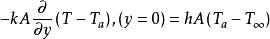努賽爾數重新書寫，得到：
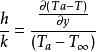努賽爾數用代表長度L相乘的方法使之成為無量綱，有：
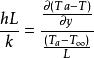努賽爾數上式右邊現在是表面溫度梯度與參考溫度梯度的比值。 而左邊與畢渥數相似。 這成為導電熱阻與流體對流熱阻的比值，稱為努塞爾數Nu。
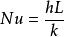努賽爾數