定義
瑕點
 瑕積分
瑕積分 瑕積分
瑕積分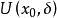 瑕積分
瑕積分 瑕積分
瑕積分 瑕積分
瑕積分 瑕積分
瑕積分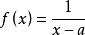 瑕積分
瑕積分 瑕積分
瑕積分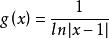 瑕積分
瑕積分如果函式在的任一鄰域內無界,則稱點為的一個瑕點。例如,是的瑕點;是的瑕點。
定義1
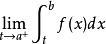 瑕積分
瑕積分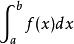 瑕積分
瑕積分設函式f(x)在(a,b]上連續,點a為f(x)的瑕點.取t>a,如果極限存在,則稱此極限為函式f(x)在(a,b]上的反常積分。瑕積分仍然記作。
定義2
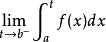 瑕積分
瑕積分設函式f(x)在[a,b)上連續,點b為f(x)的瑕點。取t<b,如果極限存在,則稱此極限為函式f(x)在[a,b)上的反常積分 。
定義3
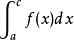 瑕積分
瑕積分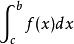 瑕積分
瑕積分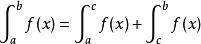 瑕積分
瑕積分設函式f(x)在[a,b]上除點c(a<c<b)外上連續,點c為f(x)的瑕點。如果兩個瑕積分與都收斂,則定義。
定理和性質
定理
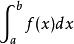 瑕積分
瑕積分 瑕積分
瑕積分 瑕積分
瑕積分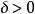 瑕積分
瑕積分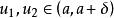 瑕積分
瑕積分瑕積分(瑕點為)收斂的充要條件是:任給存在,只要,總有
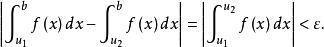 瑕積分
瑕積分性質1
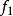 瑕積分
瑕積分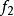 瑕積分
瑕積分 瑕積分
瑕積分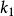 瑕積分
瑕積分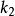 瑕積分
瑕積分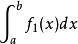 瑕積分
瑕積分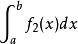 瑕積分
瑕積分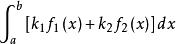 瑕積分
瑕積分設函式與的瑕點同為,、為常數,則當瑕積分與都收斂時,瑕積分必定收斂,並有
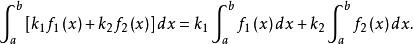 瑕積分
瑕積分性質2
 瑕積分
瑕積分 瑕積分
瑕積分 瑕積分
瑕積分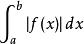 瑕積分
瑕積分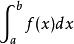 瑕積分
瑕積分設函式的瑕點為,在的任一內閉區間(a,b]上可積。則當收斂時也必定收斂,並有
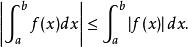 瑕積分
瑕積分性質3
 瑕積分
瑕積分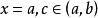 瑕積分
瑕積分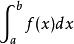 瑕積分
瑕積分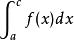 瑕積分
瑕積分設函式的瑕點為為任一常數.則瑕積分與同斂態,並有
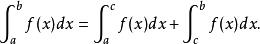 瑕積分
瑕積分收斂判別法
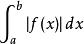 瑕積分
瑕積分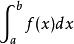 瑕積分
瑕積分當收斂時,稱為絕對收斂。稱收斂而不絕對收斂的瑕積分是條件收斂,判別瑕積分絕對收斂的比較法則如下 :
 瑕積分
瑕積分 瑕積分
瑕積分 瑕積分
瑕積分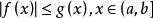 瑕積分
瑕積分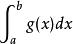 瑕積分
瑕積分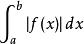 瑕積分
瑕積分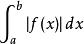 瑕積分
瑕積分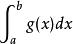 瑕積分
瑕積分( 比較法則) 設定義在(a,b]上的兩個函式與,瑕點同為,在任何[u,b]上都可積,且滿足,則當收斂時,必定收斂(或當發散時,亦必發散)。
