理想數

在數論中，理想數是在某個數域的整數環中表示一個理想的代數數。理想數的概念由恩斯特·庫默爾首先引進，並導致理察·戴德金髮展出環的理想的概念。一個整環中的理想被稱作主理想若且唯若它是由某個元素的所有倍數組成。根據主理想化定理，一個代數數域中的整環中的所有非主理想的理想在數域擴張成為一個希爾伯特類域時都會成為一個主理想。這表示存在一個類域中的整環中的元素a，其為一個理想數，即使得a 與類域中的整環中元素相乘得到的倍數與原來數域的交集就是原來的非主理想。

性質

舉例來說，設 y為方程 y+ y+ 6 = 0 的根，則擴域中的整數環為 ，即所有 a+ by形式的數，其中 a和 b為一般的整數。環中一個非主理想的例子是 ，但這個理想的立方為主理想。實際上這個環的理想類群是一個3階的循環群。與此對應的類域是添加方程 w− w− 1 = 0的根 w到而獲得的擴域：。非主理想 2 a+ yb的一個理想數是 ι = ( − 8 − 16 y− 18 w+ 12 w+ 10 y w+ y w) / 23。由於滿足 ι − 2ι + 13ι − 15ι + 16ι + 28ι + 8 = 0，它是一個代數整數。

類域的整數環中的所有乘以 ι 會得到中元素的元素都具有 aα + bβ 的形式，其中

α = ( − 7 + 9 y− 33 w− 24 w+ 3 y w− 2 y w) / 23， β = ( − 27 − 8 y− 9 w+ 6 w− 18 y w− 11 y w) / 23.。

α 和 β 也是代數整數，滿足：

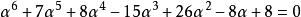理想數

和

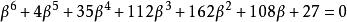理想數

同時，將 aα + bβ 乘以理想數 ι 後就會得到非主理想 2 a+ by。

歷史

庫默爾首先在1844年發表了分圓域中唯一分解定理不成立的性質。1847年，文章在約瑟夫·劉維爾的雜誌上發表。在接下來的1846年和1847年裡，庫默爾發表了他的主要定理：理想素數的唯一分解定理。

庫默爾的理想數概念在其後的四十年間被克羅內克和戴德金獨立地發展。戴德金在試圖直接推廣理想數概念時遇到了巨大的困難，最終導致他發展出了模理論和理想論。克羅內克則深化了型理論（二次型的推廣）和因子理論來解決。戴德金的理論發展成了後來的環論和抽象代數，而克羅內克的理論則成為了代數幾何中的有力工具。