詳述
例解
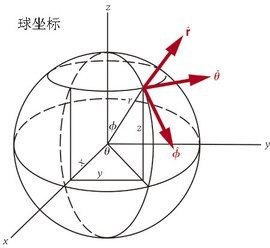
假設P（x，y，z）為空間內一點，則點P也可用這樣三個有次序的數r，φ，θ來確定，其中r為原點O與點P間的距離，θ為有向線段OP與z軸正向的夾角，φ為從正z軸來看自x軸按逆時針方向轉到OM所轉過的角，這裡M為點P在xOy面上的投影。這樣的三個數r，φ，θ叫做點P的球面坐標，顯然，這裡r，φ，θ的變化範圍為r∈[0,+∞)，φ∈[0, 2π]， θ∈[0, π] ，如圖 1所示。當r,θ或φ分別為常數時,可以表示如下特殊曲面:r = 常數，即以原點為心的球面； θ= 常數，即以原點為頂點、z軸為軸的圓錐面；φ= 常數，即過z軸的半平面。
與直角坐標系間的轉換
1).球坐標系(r,θ,φ)與直角坐標系(x,y,z)的轉換關係:
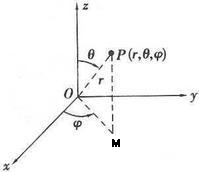圖 1 球坐標圖示x=rsinθcosφ
y=rsinθsinφ
z=rcosθ
2).反之,直角坐標系(x,y,z)與球坐標系(r,θ,φ)的轉換關係為:
r= sqrt(x*2 + y*2 + z*2);
φ= arctan(y/x);
θ= arccos(z/r);
球坐標系下的微分關係
在球坐標系中，沿基矢方向的三個線段元為：
dl(r)=dr, dl(θ)=rdθ, dl(φ)=rsinθdφ
球坐標的面元面積是：
dS=dl(θ)* dl(φ)=r^2*sinθdθdφ
體積元的體積為：
dV=dl(r)*dl(θ)*dl(φ)=r^2*sinθdrdθdφ
