定理介紹
類比圓冪定理有:
定理1
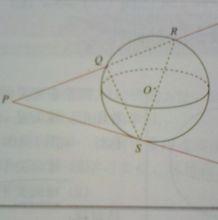
:從球面外一點P向球面引割線,交面於Q、R兩點;再從點P引球面的任一切線,切點為S,則
PS2=PQ*PR.
定理2
:從球面外一點P向球面引兩條割線,它們分別與球面相交於Q、R、S、T四點,則
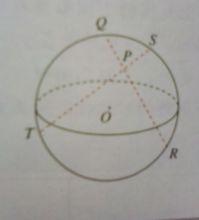 定理3
定理3PQ*PR=PS*PT.
定理3
 定理1
定理1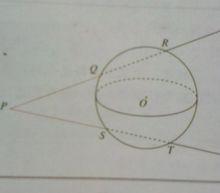 定理2
定理2:設點P是球面內一點,過點P作兩條直線,分別與球面相交於Q、R、S、T四點,則PQ*PR=PS*PT.
定理1、2、3統稱為球冪定理。
證明
具體證明可以通過P、Q、R、S、T五點在同一個平面內,劃歸為平面問題來解決,接下來的證明就和圓冪定理是一樣的了。
證明如下:
因為直線QR與ST相交於點P,所以直線QR與ST共面。又因為這兩條直線均與球O相交,所以Q、R、S、T四點共圓。然後就是圓冪定理的證明:(Q、R、S、T與下文中的A、B、C、D相對應)
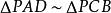 球冪定理
球冪定理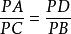 球冪定理
球冪定理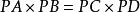 球冪定理
球冪定理圖Ⅰ:相交弦定理。如圖,AB、CD為圓O的兩條任意弦。相交於點P,連線AD、BC,由於∠B與∠D同為弧AC所對的圓周角,因此由圓周角定理知:∠B=∠D,同理∠A=∠C,所以。所以有:,即:。
圖Ⅱ:割線定理。如圖,連線AD、BC。可知∠B=∠D,又因為∠P為公共角,所以有
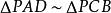 球冪定理
球冪定理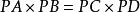 球冪定理
球冪定理,同上證得。
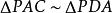 球冪定理
球冪定理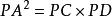 球冪定理
球冪定理圖Ⅲ:切割線定理。如圖,連線AC、AD。∠PAC為切線PA與弦AC組成的弦切角,因此有∠PBC=∠D,又因為∠P為公共角,所以有,易證
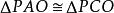 球冪定理
球冪定理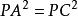 球冪定理
球冪定理圖Ⅳ:PA、PC均為切線,則∠PAO=∠PCO=90°,在直角三角形中:OC=OA=R,PO為公共邊,因此。所以PA=PC,所以。
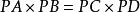 球冪定理
球冪定理綜上可知,是普遍成立的。
 圓冪定理的所有情況
圓冪定理的所有情況