球冠的公式
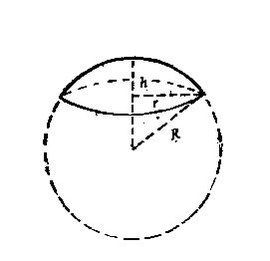
球面被平面所截得的一部分叫做球冠.截得的圓叫做球冠的底,垂直於截面的直徑被截得的一段叫做球冠的高.球冠也可以看作一段圓弧繞經過它的一個端點的直徑鏇轉所成的曲面.
公式:S=2πRh
與球冠相對應的球缺的體積公式是:(1/3)π(3R-h)×h^2 (即 πh^2(R-h/3) )
面積推導:
假定球冠最大開口部分圓的半徑為 r ,對應球半徑 R 有關係:r = Rsinθ,θ為兩直徑夾角,則有球冠積分表達:
球冠面積微分元 dS = 2πr*Rdθ = 2πR^2*sinθ dθ
積分下限為0,上限θ,
所以:S = 2πR*R(1 - cosθ)
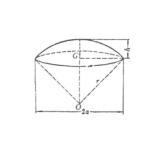 球冠
球冠其中:R(1 - cosθ)即為球冠的自身高度H
所以:S = 2πRH體積推導:
利用微元法知對應球缺與圓錐總體積為 s*r/3
減去圓錐體積即可。
球缺與球冠的區別
球缺屬於幾何體,是指用一個平面去截一個球所得的部分,是“體”的概念。而球冠只是個“面”的概念,是指一個球面被一個平面所截得的部分。
因此,球缺可以計算體積;而球冠只能計算面積。