定義
獨立性檢驗是統計學的一種檢驗方式。與適合性檢驗同屬於X2檢驗(即卡方檢驗,英文名:chi square test)它是根據次數資料判斷兩類因子彼此相關或相互獨立的假設檢驗。
假設有兩個分類變數X和Y,它們的值域分另為{x1, x2}和{y1, y2},其樣本頻數列聯表為:
| y1 | y2 | 總計 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 總計 | a+c | b+d | a+b+c+d |
若要推斷的論述為H1:“X與Y有關係”,可以利用獨立性檢驗來考察兩個變數是否有關係,並且能較精確地給出這種判斷的可靠程度。具體的做法是,由表中的數據算出隨機變數K^2的值(即K的平方)
K = n (ad - bc) / [(a+b)(c+d)(a+c)(b+d)], 其中n=a+b+c+d為樣本容量
K 的值越大,說明“X與Y有關係”成立的可能性越大。
當表中數據a,b,c,d都不小於5時,可以查閱下表來確定結論“X與Y有關係”的可信程度:
| P(K^2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K^2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
例如,當“X與Y有關係”的K 變數的值為6.109,根據表格,因為5.024≤6.109<6.635,所以“X與Y有關係”成立的機率為1-0.025=0.975,即97.5%。
與列表相關聯的概念
分類變數
其不同“值”表示相應對象所屬的不同類別的變數,分類變數的取值一定是離散的,而且不同的取值僅表示相應對象所屬的類別,如性別變數只取男、女兩個“值”,某商品的等級變數只取一級、二級、三級三個“值”,等等。分類變數的取“值”有時可用數字來表示,但這時的數字除了類別以外,沒有其他的含義。如用“0”表示“男”,用“1”表示“女”。
列聯表
分類變數的統計匯總表(頻數表)在獨立性檢驗中,一般只研究兩個分類變數,且每個分類變數只有兩個可取的值;這時得到的列聯表稱為2×2列聯表,如後面的案例中的關於患肺癌與否與吸菸與否的列聯表。
獨立性檢驗的基本思想
獨立性檢驗的必要性
獨立性檢驗的學習目標:了解獨立性檢驗的基本思想;
獨立性檢驗的學習重點:會對兩個分類變數進行獨立性檢驗。
即為什麼不能只憑列聯表中的數據和由其繪出的圖形下結論,由列聯表可以粗略地估計出兩個變數(兩類對象)是否有關(即粗略地進行獨立性檢驗),但2×2列聯表中的數據是樣本數據,它只是總體的代表,具有隨機性,故需要用獨立性檢驗的方法確認所得結論在多大程度上適用於總體。關於這一點,在後面的案例中還要進一步說明。
獨立性檢驗的原理及步驟
獨立性檢驗是一種假設檢驗(先假設,再推翻假設),它的原理及步驟與反證法類似。
反證法假設檢驗
要證明結論A想說明假設H1(兩個分類變數,即兩類對象有關)成立。在A不成立的前提下進行推理,在H1不成立,即H0(兩類對象無關,即相互獨立)成立的條件下進行推理,推出矛盾,意味著結論A成立,推出小機率事件(機率不超過α,α一般為0.001,0.01,0.05或0.1)發生,意味著H1成立的可能性很大(可能性為1-α),沒有找到矛盾,意味著不能確定A成立,沒有推出小機率事件發生,意味著不能確定H1成立。
獨立性檢驗的案例展示
案例 某醫療機構為了了解患肺癌與吸菸是否有關,進行了一次抽樣調查,共調查了9965個成年人,其中吸菸者2148人,不吸菸者7817人,調查結果是:吸菸的2148人中49人患肺癌,2099人不患肺癌;不吸菸的7817人中42人患肺癌,7775人不患肺癌。
根據這些數據能否斷定:患肺癌與吸菸有關?
【方法一】由樣本數據,可得如下列聯表和條形圖:
| 煙 \ 癌症 | 不患肺癌 | 患肺癌 | 總計 |
| 不吸菸 | 7775 | 42 | 7817 |
| 吸菸 | 2099 | 49 | 2148 |
| 總計 | 9874 | 91 | 9965 |
在不吸菸者中,患肺癌的比重是0.54%;在吸菸者中,患肺癌的比重是 2.28% 。
說明吸菸者和不吸菸者患肺癌的可能性存在較大的差異,吸菸者患肺癌的可能性大。可初步判斷:患肺癌與吸菸有關.
【方法二】以上通過對數據和圖表的分析,得到的結論是:患肺癌與吸菸有關.
但這個結論在多大程度上適用於總體呢?要回答這個問題,就必須藉助於獨立性檢驗的方法來分析.
獨立性檢驗是檢驗兩個分類變數是否有關(是否相互獨立)的一種統計方法:
用字母表示題設數據(使之更有一般性),可得如下2×2列聯表
| 煙 \ 癌症 | 不患肺癌 | 患肺癌 | 總計 |
| 不吸菸 | a | b | a+b |
| 吸菸 | c | d | c+d |
| 總計 | a+c | b+d | n=a+b+c+d |
想說明假設H1“患肺癌與吸菸有關”成立.
假設H0:H1不成立,即患肺癌與吸菸沒有關係。
在H0成立的條件下,吸菸者中不患肺癌的的比例應該與不吸菸者中相應的比例差不多,即a/(a+b)≈c/(c+d); a(c+d)≈c(a+b); ad-bc≈0。
因此|ad-bc|越小,則說明患肺癌與吸菸之間的關係越弱。
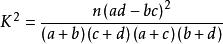 獨立性檢驗
獨立性檢驗構造統計量
作為檢驗在多大程度上可認為“兩個分類變數有關係”的標準。
若H0成立,則k2應該很小。實際上,統計學家們已經估算出如下機率:
| P(K2>K) | 0.50 | 0.40 | .025 | 0.15 | 0.10 |
| K | 0.455 | 0.708 | 1.323 | 2.072 | 2.701 |
| P(K2>K) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 5.024 | 6.637 | 7.879 | 10.828 |
這就是獨立性檢驗的臨界值表。
回到本案例,把題設數據代入公式,可得
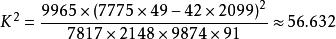 獨立性檢驗
獨立性檢驗在H0成立的情況下,P(k2≥10.828)<0.001,
即k2的值大於10.828的機率非常小(只有0.1%).
但這個小機率事件竟然發生了。
因此,我們有99.9%以上的把握認為“患肺癌與吸菸有關”。
【總結】獨立性檢驗的解題步驟如下:
第一步 提出假設H0:患肺癌與吸菸沒有關係。(目標結論H1“患肺癌與吸菸有關係”的反面)
第二步 計算獨立性檢驗的標準,即統計量k2=n(ad-bc)^2/{(a+b)(c+d)(a+c)(b+d)}的值。(它越小,原假設H0成立的可能性越大;它越大,目標結論H1成立的可能性越大。)
第三步 由獨立性檢驗的臨界值表得出結論及其可信度(即在多大程度上適用)。

