屬於傅立葉級數分析使用的條件:
(1) 函式在任意有限區間內連續,或只有有限個第一類間斷點(當t從左或右趨於這個間斷點時,函式有有限的左極限和右極限)
(2)在一個周期內,函式有有限個極大值或極小值。
(3) x(t)在單個周期內絕對可積,即
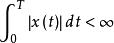 狄里赫利條件
狄里赫利條件關於傅立葉級數和傅立葉積分可以參考《高等數學》
狄里赫利條件屬於傅立葉級數分析使用的條件。傅立葉在提出傅立葉級數時堅持認為,任何一個周期信號都可以展開成傅立葉級數,雖然這個結論在當時引起許多爭議,但持異議者卻不能給出有力的不同論據。直到20年後(1829年)狄里赫利才對這個問題作出了令人信服的回答,狄里赫利認為,只有在滿足一定條件時,周期信號才能展開成傅立葉級數。
屬於傅立葉級數分析使用的條件:
(1) 函式在任意有限區間內連續,或只有有限個第一類間斷點(當t從左或右趨於這個間斷點時,函式有有限的左極限和右極限)
(2)在一個周期內,函式有有限個極大值或極小值。
(3) x(t)在單個周期內絕對可積,即
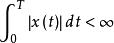 狄里赫利條件
狄里赫利條件關於傅立葉級數和傅立葉積分可以參考《高等數學》
狄利赫里條件是指給定的周期函式在有限的區間內,只有有限個第一類間斷點和有限個極大值和極小值。
狄利克雷條件是一個信號存在傅立葉變換的充分不必要條件。 狄利克雷條件括三方面: (1 )在一周期內,連續或只有有限個第一類間斷點; (2)在一周期內,極...
背景 定義 間斷點 傅立葉變換《太空堡壘卡拉狄加》(Battlestar Galactica)是一出在2003年12月8日於美國科幻頻道(Sci Fi Channel)上開播的美國科...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮阿佛洛狄忒(希臘語:Αφροδίτη;英語;Aphrodite)是古希臘神話中的愛與美之女神,是奧林帕斯十二主神的一柱,在羅馬神話中被稱為維納斯。阿弗洛...
人物簡介 神話故事 愛情詛咒 文學歌頌 倍受尊敬阿佛洛狄忒(希臘語:Αφροδίτη;英語;Aphrodite)是古希臘神話中的愛與美之女神,是奧林帕斯十二主神的一柱,在羅馬神話中被稱為維納斯。阿弗洛...
人物簡介 神話故事 愛情詛咒 文學歌頌 倍受尊敬在羅馬神話中與阿芙羅狄忒相對應是維納斯(拉丁語:Venus)。專司女性魅力與美貌的愛與美之女神。阿芙羅狄忒曾經愛上人間的一位獵人阿多尼斯,他英俊、體貼、...
阿芙羅狄忒 神話 文化衍生阿佛洛狄忒(希臘語:Αφροδίτη;英語;Aphrodite)是古希臘神話中的愛與美之女神,是奧林帕斯十二主神的一柱,在羅馬神話中被稱為維納斯。阿弗洛...
人物簡介 神話故事 愛情詛咒 文學歌頌 倍受尊敬《太空堡壘卡拉狄加》()是美國科幻頻道出品的一部軍事科幻電視劇,由羅納德·D·摩爾所創作,根據1978年同名電視劇改編而成。該劇包括一部迷你劇與四季正劇...
劇情簡介 分集劇情 演職員表 角色介紹 幕後花絮尼祿,全名尼祿·克勞狄烏斯·愷撒·奧古斯都·日耳曼尼庫斯(拉丁語:Nero Claudius Caesar Augustus Germanicus,公元...
家世 統治 婚姻 反叛 窮途末路