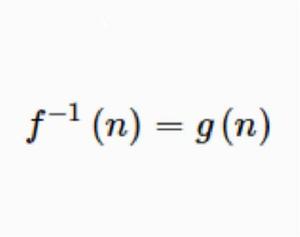基本介紹
設f(n)為數論函式，若存在數論函式g(n)，使得f*g=I，則稱g(n)為f(n)的狄利克雷逆，或簡稱逆，記為f(n)=g(n)。例如，μ*U=I，故U(n)的逆μ(n)=U(n)≡1。反之，U(n)≡1的逆U(n)=μ(n)，從定義及交換律可知，若g為f的逆，則f亦為g的逆，即若g=f，則f=g。
狄利克雷逆的性質
狄利克雷逆有下述性質：
1.若數論函式f(n)滿足f(1)≠0，則存在惟一的逆f(n)，且滿足
f(1)=1/f(1)，
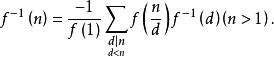狄利克雷逆故知積性函式f必有逆f，且f仍為積性函式。
2.若數論函式f(n)，g(n)滿足f(1)≠0，g(1)≠0，則(f*g)=f*g。
3.若f(n)為積性函式，則f(n)為完全積性函式的充分必要條件是f(n)=μ(n)f(n)。特別地，當g(n)為完全積性函式，且h=f*g時，有f=h*μg。
重要的狄利克雷逆
重要的狄利克雷逆有：
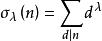狄利克雷逆設 ，則
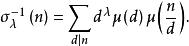狄利克雷逆特別地，當λ=0或1時，得到
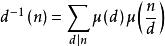狄利克雷逆及
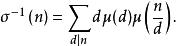狄利克雷逆
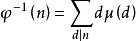狄利克雷逆2.設φ(n)為歐拉函式，則 .
3.默比烏斯函式μ(n)的逆μ(n)=U(n)≡1。
4.劉維爾函式λ(n)的逆λ(n)=μ(n)λ(n)。
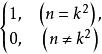狄利克雷逆5.設g(n)=λ*U= ，則
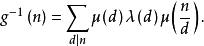狄利克雷逆