人物簡介
狄利克雷（1805～1859） Dirichlet，Peter Gustav Lejeune 德國數學家。對數論、數學分析和數學物理有突出貢獻，是解析數論的創始人之一。1805年2月13日生於迪倫，1859年5月5日卒于格丁根。中學時曾受教於物理學家G.S.歐姆；1822～1826年在巴黎求學，深受J.-B.-J.傅立葉的影響 。回國後先後在布雷斯勞大學、柏林軍事學院和柏林大學任教27年，對德國數學發展產生巨大影響。1839年任柏林大學教授，1855年接任C.F.高斯在哥廷根大學的教授職位。
在分析學方面，他是最早倡導嚴格化方法的數學家之一。1837年他提出函式是x與y之間的一種對應關係的現代觀點。
在數論方面，他是高斯思想的傳播者和拓廣者。1836年狄利克雷撰寫了《數論講義》，對高斯劃時代的著作《算術研究》作了明晰的解釋並有創見，使高斯的思想得以廣泛傳播。1837年，他構造了狄利克雷級數。1838～1839年，他得到確定二次型 類數的公式。1846年，使用抽屜原理。闡明代數數域中單位數的阿貝爾群的結構。
在數學物理方面，他對橢球體產生的引力、球在不可壓縮流體中的運動、由太陽系穩定性導出的一般穩定性等課題都有重要論著。1850年發表了有關位勢理論的文章，論及著名的第一邊界值問題，現稱狄利克雷問題。
豪斯多夫空間
在拓撲學和相關的數學分支中，豪斯多夫空間、分離空間或T2 空間是其中的點都“由鄰域分離”的拓撲空間。在眾多可施加在拓撲空間上的分離公理中，“豪斯多夫條件”是最常使用和討論的。它蘊涵了序列、網和濾子的極限的唯一性。豪斯多夫得名於拓撲學的創立者之一費利克斯·豪斯多夫。豪斯多夫最初的拓撲空間定義把豪斯多夫條件包括為公理。
假設 X 是拓撲空間。設 x 和 y 是 X 中的點。我們稱 x 和 y 可以“由鄰域分離”，如果存在 x 的鄰域 U 和 y 的鄰域 V 使得 U 和 V 是不相交的 (U ∩ V = ∅)。X 是豪斯多夫空間如果任何兩個X 的獨特的點可以由鄰域分離。這時的豪斯多夫空間也叫做 T2 空間和分離空間的原因。
X 是預正則空間，如果任何兩個拓撲可區分的點可以由鄰域分離。預正則空間也叫做 R1 空間。
在這些條件之間的聯繫如下。拓撲空間是豪斯多夫空間，若且唯若它是預正則空間和柯爾莫果洛夫空間的二者(就是說獨特的點是拓撲可區分的)。拓撲空間是預正則空間，若且唯若它的柯爾莫果洛夫商空間是豪斯多夫空間。
狄利克雷空間論
狄利克雷空間論 狄利克雷空間論 狄利克雷空間論 狄利克雷空間論 狄利克雷空間論設X是局部緊的豪斯多夫空間，為X上一個處處稠密的正拉東測度(對任意非空開集G,(G)>0)。若X上局部可積的復值函式u組成的希爾伯特空間D=D(X,)滿足下述三條公理，則稱D(X,)是狄利克雷空間：
對任意緊集K，存在實數A(K)>0，使得
1.對任意緊集K，存在實數A(K)>0，使得
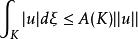狄利克雷空間論2.C(X)∩D(X，ξ)在C(X)及D(X，ξ)中稠密。
3.對複平面上任一正常的壓縮映射T和任一u∈D(X，ξ)，有T∈D且‖T‖≤‖u‖。
若對於u∈D(X，ξ)，存在拉東測度μ，使得：
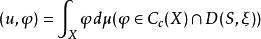狄利克雷空間論
狄利克雷空間論則稱u為的位勢。在狄利克雷空間論中，也有相應的掃除原理、平衡原理和電容器原理等。
