簡介
狄氏型理論是公理化位勢論的一種形式，是狄利克雷空間論的進一步發展。
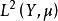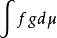狄氏型理論
狄氏型理論狹義的狄氏型理論是指定義在如下希爾伯特空間的一個稠密子空間D(E)上的、滿足一定條件的雙線性泛函E，即(Y,)是一個可測空間，μ是(Y,)上σ有限測度，Y上定義的、關於μ平方可積的數值函式（等價類）全體關於為內積構成的希爾伯特空間記為L (Y,μ)。
公理化位勢論
(axiomatic potential theory)
公理化位勢論是在抽象空間裡通過設定公理的方法建立起來的位勢理論。
公理化體系大致可分成三類。第一類是調和空間論，第二類是狄氏型（又稱狄利克雷形式），第三類是非線性公理體系。相對第三類而言，第一、二類都屬於線性公理體系。由於位勢論的大部分結果都可由其三個基本原理（即狄利克雷問題、極小值原理和收斂性質）導出，且為了適應偏微分方程和隨機過程的需要，公理化位勢論迅速地發展起來，它提供了統一處理問題的方法。
狄利克雷空間論
(theory of Dirichlet space)
狄利克雷空間論是受BLD函式組成的希爾伯特空間論的啟發，在狄利克雷空間上建立的一種公理位勢論。
在狄利克雷空間論中，也有相應的掃除原理、平衡原理和電容器原理等。
