定義
特徵根法是解常係數線性微分方程的一種通用方法。
特徵根法也可用於通過數列的遞推公式(即差分方程,必須為線性)求通項公式,其本質與微分方程相同。
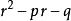 特徵根法
特徵根法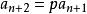 特徵根法
特徵根法稱為二階齊次線性差分方程: 加權的特徵方程。
利用特徵根法解方程
對微分方程:
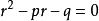 特徵根法
特徵根法設特徵方程 兩根為 r、 r。
① 若實根 r不等於 r
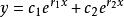 特徵根法
特徵根法.
② 若實根 r= r
③ 若有一對共軛復根 a± bi
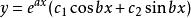 特徵根法
特徵根法對差分方程:
1) 若特徵方程有兩個不等實根 r、 r
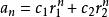 特徵根法
特徵根法則
其中常數 c、 c由初始值 a= a、 a= b 唯一確定。
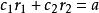 特徵根法
特徵根法(1)
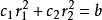 特徵根法
特徵根法(2)
2) 若特徵方程有兩個相等實根 r= r= r
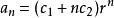 特徵根法
特徵根法其中常數 c、 c由初始值唯一確定。
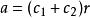 特徵根法
特徵根法(1)
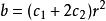 特徵根法
特徵根法(2)
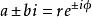 特徵根法
特徵根法3 )若特徵方程有一對共軛復根,則有
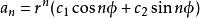 特徵根法
特徵根法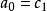 特徵根法
特徵根法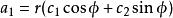 特徵根法
特徵根法一類重特徵根對方程解的簡便解法
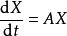 特徵根法
特徵根法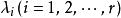 特徵根法
特徵根法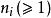 特徵根法
特徵根法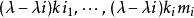 特徵根法
特徵根法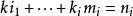 特徵根法
特徵根法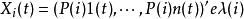 特徵根法
特徵根法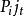 特徵根法
特徵根法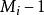 特徵根法
特徵根法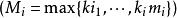 特徵根法
特徵根法對於常係數齊次線性微分方程組 ,當矩陣 A的特徵根 的重數是 ,對應的 m個初等因子是 , 時,它對應方程中ni個線性無關解,其結構形如 ,此時多項式 的次數小於等於 , 。
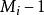 特徵根法
特徵根法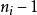 特徵根法
特徵根法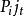 特徵根法
特徵根法由於 M計算起來非常困難,本文利用相似矩陣的特點和Jordan標準型在 與 之間找到了一個便於套用的多項式 次數的上界,使計算起來更加方便和有效。

