簡介
概述
在力學中研究質點的機械運動時，我們用位置矢量與運動速度（動量）來描述質點的運動狀態，而在討論由大量作無規則熱運動的分子所構成的物質的狀態時，我們不可能一個一個的描述每個分子的位置矢量與運動速度（動量）。（根據海森堡不確定原理，我們不能同時確定微觀粒子的位置矢量與動量。）而且每個分子的位置矢量與運動速度（動量）也是沒有太大意義的，它們只能用來描述氣體分子微觀運動的運動狀態，並不能反映整個氣體的巨觀狀態。用來描述分子熱運動的巨觀物理量叫做物態參量。
氣體的物態參量
用氣體來舉例，對一定量的氣體，其巨觀狀態可以用氣體的體積V、壓強p和溫度T來描述，氣體的體積、壓強、溫度這三個物理量稱為氣體的物態參量。
體積
氣體的體積是指氣體分子所能達到的空間，對於容器中的氣體而言，容器的體積即氣體的體積，在國際單位之中體積的單位為m。
壓強
氣體的壓強是作用在容器器壁上單位面積的正壓力，從微觀上看是器壁單位面積上氣體分子與器壁碰撞的平均作用力。在國際單位制中，壓強的單位為帕斯卡（Pa）。
溫度
溫度是物體冷熱程度的量度，溫度反映了氣體分子熱運動的激烈程度。溫度的數值表達方法稱作溫標。國際計量大會規定熱力學溫標為基本溫標，單位為開爾文（K）。在我國日常生活中常用攝氏溫標，攝氏溫度用符號t表示。單位為攝氏度（℃）。
這三個描述氣體狀態的物態參量都是巨觀物理量，而組成氣體的分子所具有的質量、速度、動量、體積等描述個別分子的物理量都是微觀物理量。描述氣體狀態的巨觀物態參量與微觀物理量間存在一定的對應關係。
函式關係
物態方程
處於平衡態的氣體，物態參量p、V、T間有一定的函式關係。忽略氣體分子的自身體積，將分子看成是有質量的幾何點；假設分子間沒有相互吸引和排斥，分子之間及分子與器壁之間發生的碰撞是完全彈性的，不造成動能損失。這種氣體稱為理想氣體。一般，在壓強較低，溫度不是特別低的情況下氣體可以視作理想氣體。
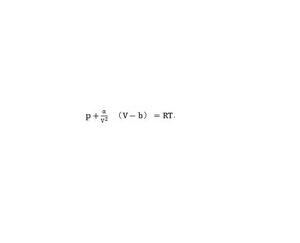范德瓦爾斯物態方程實際氣體由於分子間相互作用力，方程pV=nRT的p和V需要一個修正。修正之後，物態方程稱作范德瓦爾斯物態方程，如右下圖：
物態方程的意義
由於每一個體系的組成和物理性質均不一祥，所以得到的每一個物態方程各不相同，毎一個物態方程只有對處於平衡狀態下的均勻體系計算出來，而非平衡態或非均勻體系的物態方程無法表示出來。因此可以說物態方程表示處於平衡態的均勻系統的各狀態參量之間的函式關係，通過物態方程使用實驗中得到的一些數據來可以計算出體系的很多無法測量的物理量。此外，在 很多理論計算過程中利用物態方程可以簡化計算過程或者對 一些規律的提出起到基本性的作用。
