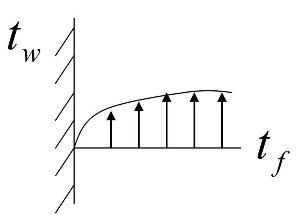
定義
如圖所示
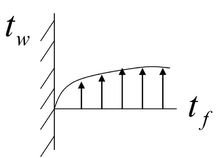牛頓冷卻定律溫差Δt=|tw-tf|
q=hΔt
Φ=qA=AhΔt=Δt/（1/hA)
其中的1/hA 稱為對流傳熱熱阻
字母代碼
q為熱流密度
h為物質的對流傳熱係數
Φ為傳熱功率（或者說是單位時間內的傳熱量）A為傳熱面積
一個熱的物體的冷卻速度與該物體和周圍環境的溫度差成正比。
分析
即-dT/dt=(T-Tc)/τ式中，-dT/dt——物體的溫度隨時間下降的速度，負號表示物體的溫度是下降的τ——物體的溫度從T 下降到環境溫度Tc實際所需要的弛豫時間在微分條件下，-dT/dt和(T-Tc)/τ是微線性關係。這是微線性思維的典範之一。
牛頓冷卻定律的這個微分方程沒有考慮物體的性質，所以這不是物性方程式。它只是關於一個假想物體，其溫度隨時間單純下降的一個數學微分方程。與其叫“牛頓冷卻定律”，毋寧叫“牛頓冷卻定理”更準確。不過，這個明顯的缺點，反而是最大的優點。它的無比抽象性在宣告：“這是任何物體冷卻的共同遵守的數學規律！”。
實驗表明
物體的溫度隨時間下降的速度和物體的結構以及理化性質並非完全無關。尤其是急速冷卻的條件下，我們可以修改線性“牛頓冷卻定理”，給它添加若干個非線性的項就可以解決實際問題了。
這也告訴我們上面的微線性牛頓冷卻定律至少不適用於描寫那些急速溫度變化的物理現象。
解方程可得牛頓冷卻定律的積分形式為
Δt=t-to=τln(To-Tc)/(T-Tc)
或者 exp（Δt/τ）=To-Tc/T-Tc
式中，To——為物體在初始時刻to的溫度
Δt>0，這是必然的。為此，必然有 To>T>Tc。
這就是說，物體的起始溫度To必然大於它最後的冷卻溫度T；物體最後的冷卻溫度T不能比環境溫度Tc更低，而且也不能被冷卻到和環境溫度一樣低。我們可以假設最後的冷卻溫度非常接近環境溫度，
這時，T-Tc=ΔT，ΔT>0，且ΔT→0。也就是說，溫度ΔT是一個極小的正值。
設熱水的冷卻方程為：exp（Δt/τ）=To-Tc/T-Tc
設冷水的冷卻方程為：exp（Δt`/τ`)=To`-Tc`/T`-Tc`
假設，熱水和冷水的起始時刻一致to=to`，冷卻的環境溫度一致Tc=Tc`，熱水比冷水的起始溫度高，To>To`，熱水和冷水最後的狀態幾乎一致，即熱水和冷水最後的溫度與環境的溫度差無窮逼近——即近似相等，ΔT=T-Tc=ΔT`=T`-Tc。
熱水和冷水方程之比：exp（Δt/τ）/exp（Δt`/τ`)=To-Tc/To`-Tc
=exp(C)>1（即 C>0)
於是，Δt/τ - Δt`/τ` = C
Δt=（τ/τ`）Δt`+ C
這是一個截距和斜率都為正值的直線方程，
如果熱水比冷水先結冰，Δt<；Δt`，必須有 τ<；τ`。即斜率τ/τ`<1。
如果冷水比先熱水結冰，Δt>；Δt`，必須有 τ>；τ`。即斜率τ/τ`>1。
這個結果表明：牛頓冷卻定律並不能直接用來判斷熱水和冷水誰先結冰。
而且熱水和冷水無論誰先結冰，都不會影響牛頓冷卻定律的正確性。
牛頓冷卻定律
牛頓冷卻定律（Newton's law of cooling)：溫度高於周圍環境的物體向周圍媒質傳遞熱量逐漸冷卻時所遵循的規律。當物體表面與周圍存在溫度差時，單位時間從單位面積散失的熱量與溫度差成正比，比例係數稱為熱傳遞係數。牛頓冷卻定律是牛頓在1701年用實驗確定的，在強制對流時與實際符合較好，在自然對流時只在溫度差不太大時才成立。
是傳熱學的基本定律之一，用於計算對流熱量的多少。
如圖所示：
溫差Δt＝|tw-tf|
q＝hΔt
Φ＝qA＝AhΔt＝Δt/(1/hA)
其中的1/hA 稱為對流傳熱熱阻
字母代碼：
q為熱流密度
h為物質的對流傳熱係數
Φ為傳熱量A為傳熱面積
冷卻定律
對於同一物體溫度下降的速率,牛頓做過研究,並發現同一物體在外部介質性質及溫度相同,本身性質及表面積相同時,物體冷卻的速率只與外部與物體的溫差有關.
一個較周圍熱的物體溫度為T,忽略表面積以及外部介質性質和溫度的變化.它的冷卻速率(dT/dt)與 該物體的溫度與周圍環境的溫度C的差(T-C)成正比.即dT/dt=-k(T-C).其中,t為時間,k為一個常數.
計算方法是:
對 dT/dt=-k(T-C) 進行積分,得
ln(T-C)=-kt+B(B為積分常數)
(T-C)=e^(-kt+B) (1)
設t=0,也就是物體的初溫,(1)變成
(T0-C)=e^B
然後代入 (1) 得
T=C+(T0-C)×e^(-kt)
算出B與k,代入t的值,就可以算出某個時間物體的溫度.
冷卻定律推導出來,在忽略表面積以及外部介質性質和溫度的變化,物體溫度變化是越來越慢的.
對權威的牛頓冷卻定律提出挑戰
中學生姆潘巴的精心觀察對權威的牛頓冷卻定律提出挑戰
我（姆潘巴）在坦尚尼亞的馬乾巴中學讀三年級時，校中的孩子們做冰淇淋總是先煮沸牛奶，待到冷卻後再倒入冰盤，放進電冰櫃。為了爭得電冰櫃的最後一隻冰盤，我決心冒著弄壞電冰櫃的風險而把熱牛奶放進去了。一個多小時以後，我們打開電冰櫃，裡面出現了驚人的奇蹟：我的冰盤裡的熱牛奶已結成堅硬的冰塊，而他們的冰里還是稠稠的液體。我飛快地跑去問物理老師，他淡淡地回答說：“這樣的事一定不會發生。”
進入高中後，在學習牛頓冷卻定律時，我又問物理老師，他同樣輕率地否定了我的觀察。我繼續述說我的理由，可老師不願意聽，在一旁的同學們也幫著老師質問我：“你究竟相不相信牛頓冷卻定律？”我只好為自己辯解：“可定律與我觀察的事實不符嘛！”在同學們的訕笑聲中，老師帶著無可奈何的神情說道：“你說的這些就叫做姆潘巴的物理吧！”從此以後，“姆潘巴的物理”便成了我的綽號，只要我做錯一點，同學們就馬上說“這是姆潘巴的什麼……。”儘管如此，我仍然堅信我的觀察是正確的，其中可能包含著更為深刻的道理。
就在這一年，坦尚尼亞最高學府三蘭港大學物理系系主任奧斯波恩博士來我校訪問，我決心求助於博士，我向他講述了我的奇遇。他先是笑了一下，然後認真地聽取了我的複述，博士回校後親自動手並觀察到了同一事實。他高度評價了我的觀察，他說：“姆潘巴的觀察，事實上提出了權威物理學家可能遇到的危險，同時也對物理教師提出了一個感興趣的問題。”
論文介紹
博士邀請我聯名發表一篇論文，登載於《英國教育》，對熱牛奶在電冰櫃中先行凍結的現象作了介紹和解釋。其主要內容是：
1．把牛奶換成水以後再進行觀察，發現電冰櫃中的熱水仍在冷水之前凍結成冰。
2．把熱水放入電冰櫃冷卻時，水的上表面（S）與底部（B）之間存在著顯著的溫度差。緩慢冷卻時的溫度差幾乎是觀察不到的。圖1-1是初始溫度分別為70℃（實線）和47℃（虛線）的水的S-B溫度差隨時間變化的觀測記錄圖。從圖中可看出，初始時，上表面與底部不存在溫度差，但一經急劇冷卻，溫度差就立即出現，其中初溫為70℃的水內產生的最高溫度差接近14℃,而初溫為47℃的水內產生的最高溫度差只有10℃左右，這就是我們所觀察到的冷、熱水在急劇冷卻時的重大差別。
相關解釋
在以上定量觀測的基礎上，我們對熱牛奶（或熱水）先凍結的現象作出如下解釋：
1．冷卻的快慢不是由液體的平均溫度決定的，而是由液體上表面與底部的溫度差決定的，熱牛奶急劇冷卻時，這種溫度差較大，而且在整個凍結前的降溫過程中，熱牛奶的溫度差一直大於冷牛奶的溫度差。
2．上表面的溫度愈高，從上表面散發的熱量就愈多，因而降溫就愈快。
基於以上兩方面的理由，熱牛奶以更高的速度冷卻著，這便是熱牛奶先凍結的秘密。
除了作出熱牛奶先凍結的解釋外，我們還大膽地類推出一個有趣的“猜想”：在發生嚴重冰凍的日子裡，熱水管應該先於冷水管發生凍結，是不是這樣呢？由於我們生活在赤道附近的坦尚尼亞，這裡氣候四季炎熱，難以觀察到這十分有趣的現象，歡迎能觀察到這一現象的中學朋友們，為我們提供信息，共同討論。
自從我們的文章發表後，世界上很多科學雜誌都刊登了這一自然現象，認為這是對牛頓冷卻定律的嚴峻挑戰。而且還以我的名字把這一自然現象命名為“姆潘巴效應”。這真叫人不好意思呀！
反思
中學生姆潘巴觀察到的現象，可能好多人都遇到過，但是為什麼會發生姆潘巴的同學不相信，老師不相信，甚至連物理學博士聽後也還是“先笑了一下”呢？他們可能是這樣思考的：
冷牛奶從初溫開媽到凍結所需時間為t1，熱牛奶冷卻到初溫所需時間t2，則熱牛奶從初溫開始到凍結所需的全部時間為t1+t2。
顯然有（t1+t2）>t1.
由上式可以推導出如下結論：熱牛奶先凍結的現象不可能發生。
如果發生了熱牛奶先凍結的現象，則必然導出（t1+t2）
正因為上述貌似正確的推理支配著人們的頭腦，所以不少的人不但自己不去觀察，甚至連別人觀察到的事實也不敢相信。這種不尊重觀察的態度，往往使真理從自己的鼻尖下面悄悄溜走，這難道不值得立志從事科研工作的人們引以為戒嗎？
事實上，在一般實驗條件下，熱水會比冷水更快結冰。這種現象違反直覺，甚至連很多科學家也感到驚訝。但它的確是真的，曾在很多實驗觀察和研究過。雖然在經過亞里斯多德、培根，和笛卡兒 [1- 3] 三人的介紹後，此現象已被發現了幾個世紀，但卻一直沒有被引入現代科學。直至1969年，才由坦尚尼亞的一間中學的一個名叫 Mpemba 的學生引入現代科學。這個效應早期發現史，和後期 Mpemba 再發現的故事－－尤其是後者，都是充滿戲劇性的寓言。寓意人們在判斷什麼是不可能時，別過於倉促。這一點，下面會說到。
Mpemba效應
熱水比冷水更快結凍的現象通常叫「Mpemba 效應」。無疑地，很多讀者對這一點很懷疑，因此，有必要先明確地指出，什麼是 Mpemba 效應。有兩個形狀一樣的杯，裝著相同體積的水，唯一的分別是水的溫度。現在將兩杯水在相同的環境下冷卻。在某些條件下，初溫較高的水會先結冰，但並不是在任何情況下，都會這樣。例如，99.9° C 的熱水和 0.01° C 的冷水，這樣，冷水會先結冰。Mpemba 效應並不是在任何的初始溫度、容器形狀、和冷卻條件下，都可看到。
這似乎是不可能的，不少敏銳的讀者可能已經想出一個方法，去證明它不可能。這種證明通常是這樣的： 30° C 的水降溫至結冰要花 10 分鐘， 70° C 的水必須先花一段時間，降至 30° C，然之後再花 10 分鐘降溫至結冰。由於冷水必須做過的事，熱水也必須做，所以熱水結冰較慢。這種證明有錯嗎？
這種證明錯在，它暗中假設了水的結冰只受平均溫度影響。但事實上，除了平均溫度，其它因素也很重要。一杯初始溫度均勻，70° C 的水，冷卻到平均溫度為 30° C 的水，水已發生了改變，不同於那杯初始溫度均勻，30° C 的水。前者有較少質量，溶解氣體和對流，造成溫度分布不均。這些因素亦會改變冰櫃內，容器周圍的環境。下面會分別考慮這四個因素。所以前面的那種證明是行不通的，事實上，Mpemba 效應已在很多受控實驗中觀察到 [5,7-14]。
這種現象的發生機制，仍然沒有得確切的了解。雖然有很多可能的解釋已被提出過，但到目前為止，還沒有一個實驗可以清晰地顯示它的機制。如果有的話，這實驗就十分重要了。你可能會聽到有人很自信地說，X 是 Mpemba 效應的原因。這些說法通常都是基於猜測，或只看著小量文獻的證據，而忽略其它。當然，有根據地猜測，和選擇你信賴的實驗結果，是沒錯的。問題是，對於什麼是 X，不同的人提出不同的說法。
蒸發
——在熱水冷卻到冷水的初溫的過程中，熱水由於蒸發會失去一部分水。質量較少，令水較容易冷卻和結冰。這樣熱水就可能較冷水早結冰，但冰量較少。如果我們假設水只透過蒸發去失熱，理論計算能顯示蒸發能解釋 Mpemba 效應 。這個解釋是可信的和很直覺的，蒸發的確是很重要的一個因素。然而，這不是唯一的機制。蒸發不能解釋在一個封閉容器內做的實驗，在封閉的容器，沒有水蒸氣能離開 。很多科學家聲稱，單是蒸發，不足以解釋他們所做的實驗 [5,9,12]。
溶解氣體
——熱水比冷水能夠留住較少溶解氣體，隨著沸騰，大量氣體會逃出水面。溶解氣體會改變水的性質。或者令它較易形成對流（因而令它較易冷卻），或減少令單位質量的水結冰所需的熱量，又或改變凝固點。有一些實驗支持這種解釋 [10,14]，但沒有理論計算的支持。
對流
——由於冷卻，水會形成對流，和不均勻的溫度分布。溫度上升，水的密度就會下降，所以水的表面比水底部熱——叫「hot top」。如果水 主要透過表面失熱，那么「hot top」的水失熱會比溫度均勻的快。當熱水冷卻到冷水的初溫時，它會有一「hot top」因此與平均溫度相同，但溫度均勻的水相比，它的冷卻速率會較快。能跟上嗎？你可能想重看這一段 ，小心區分初溫、平均溫度，和溫度。雖然在實驗中，能看到「hot top」和相關的對流，但對流能否解釋 Mpemba 效應，仍是未知。
周圍事物
——兩杯水的最後的一個分別，與它們自己無關，而與它們周圍的環境有關。初溫較高的水可能會以複雜的方式，改變它周圍的環境，從而影響到冷卻過程。例如，如果這杯水是放在一層霜上面，霜的導熱性能很差。熱水可能會熔化這層霜，從而為自己創立了一個較好的冷卻系統。明顯地，這樣的解釋不夠一般性，很多實驗都不會將容器放在霜層上。
試驗表明
最後[supercooling]在此效應上，可能是重要的。[supercooling]現象出現在水在低於 0° C 時才結凍的情形。有一個實驗 發現，熱水比冷水較少會[supercooling]。這意味著熱水會先結冰，因為它在較高的溫度下結冰。即使這是真的，也不能完成解釋 Mpemba 效應，因為我們仍需解釋為什麼熱水較少會[supercooling]。
簡單地說，在很多情況下，熱水較冷水先結冰。這並非不可能，在很多實驗中已觀察到。然而，儘管有很多說法，但仍沒有一個很好的解釋。有不同的機制曾被提出，但這些實驗證據都不是決定性的。
