簡介
與剛體運動比較,流體質點運動的最大不同點,是除了可有平動、轉動、或平移帶轉動外,還可能有變形出現。變形特性取決於流速場特性,或線性變形(拉伸、壓縮),或角變形。因此,就一般情況而言,流體運動可分解為位移、旋轉和變形三種基本形式。其中變形對質點應力分析有重大影響,而旋轉與否,其流動規律完全不同。
液流中各液體微團的旋轉角速度都為0,因而不存在旋轉運動的流動稱為無旋流,無旋流中:
 無旋流
無旋流 無旋流
無旋流反之,液流中如有液體微團作旋轉運動,亦即旋轉角速度不全為0,則這種液體運動叫做有旋流,在有旋流運動中,上述三個等式至少有一個得不到滿足。實際上,往往是一部分流場可以是有旋流,另一部分可以是無旋流。
 有旋流
有旋流必須注意,流動究竟是無旋流還是有旋流,是根據液體微團的本身是否旋轉而決定的,並不是由該微團的軌跡形狀而定的。 例如右圖所示的運動,微團的軌跡為一圓周,但微團本身並無旋轉,故為無旋流。而在所示的運動,微團的軌跡線是一直線,但微團本身卻在轉動,故為有旋流。
無旋流的“勢”
無旋流動的基本特徵是流速場必須滿足
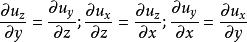 無旋流
無旋流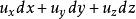 無旋流
無旋流 無旋流
無旋流由高等數學得知,該式是使表達式為某一函式的全微分的必要和充分條件,因此對無旋流講,必然存在下列關係
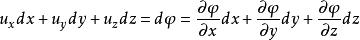 無旋流
無旋流由此可得
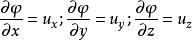 無旋流
無旋流 無旋流
無旋流 無旋流
無旋流無旋流動中存在的這一標量場,與力場中的力勢相對比,有同樣形式的關係,故函式稱為“流速勢”,無旋流又稱為有勢流動。在分析勢流 時,由於流速勢與流速分量之間具有如上所述的關係;因此,只需求出流速勢,便可立即得到三個流速分量,對求解勢流問題,提供了極大的方便。
無旋流動是一種理想的運動狀態,在實際液流中,由於粘滯性的作用,一般為有旋流。

