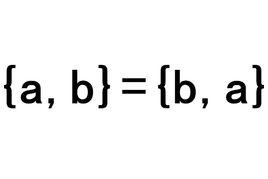無序對

亦稱二元集.公理集合論術語.指由兩個元素構成的集合.通常記為a,b,a,b為其元素.若a=b,則a,b只包含一個元素,稱其為單點集,記為a.由無序對公理,任何兩個集合均可構成一個二元集.在無序對中,兩個元素無先後次序,即a,b=b,a,這正是無序對一名的由來 。

定義

定義{xy}={x}U{y}．類[xy]稱為無序對(unordered pair) 。

無序對(unordered pair)一種特殊的集合.即僅含兩個元素的集合.對於任意的兩個對象(集合))u與v，集合{u,v}={v,u}稱為對象u與v的無序對.由於u,v是任意的兩個對象，u與v既可以相同也可以不同。當u=v時，{u,v}可以記為{u}或{v}，集合{u}或{v}稱為單元集，即僅含有一個元素的集合.單元集是無序對集合的一種特殊情況 。

舉例

恰好有二個元素的集合，並且這二個元素之間沒有一定順序的，叫做無序對集合．比如，前邊提到的{1，2}就是一個無序對集合，對於{1,2}，還可以寫作{2,1}．也就是說，

我們有

{1,2}={2,1}

對於任意的對象a、b，無序對集合{a,b}都等於{b,a}另外，{ N, Q},{1， N},{ R, N}都是無序對集合。

還應當注意，就是{1,2，3}={1,2}。在任一集合中，某一個元素重複出現多次和它只出現一次，其結果沒有變化，仍然是相同的集合。因此，{a,a}就是單元集合{a}，{a,a,a}還是單元集合{a}；而{a,a,b}，{b,b,a,a}也仍然是無序對集合{a,b} 。