理論提出
首先是由華中科技大學的鄧聚龍教授提出的理論。
理論概念
灰色預測是一種對含有不確定因素的系統進行預測的方法。灰色預測通過鑑別系統因素之間發展趨勢的相異程度,即進行關聯分析,並對原始數據進行生成處理來尋找系統變動的規律,生成有較強規律性的數據序列,然後建立相應的微分方程模型,從而預測事物未來發展趨勢的狀況。其用等時距觀測到的反應預測對象特徵的一系列數量值構造灰色預測模型,預測未來某一時刻的特徵量,或達到某一特徵量的時間。
分類
①灰色時間序列預測;即用觀察到的反映預測對象特徵的時間序列來構造灰色預測模型,預測未來某一時刻的特徵量,或達到某一特徵量的時間。
②畸變預測;即通過灰色模型預測異常值出現的時刻,預測異常值什麼時候出現在特定時區內。
③系統預測;通過對系統行為特徵指標建立一組相互關聯的灰色預測模型,預測系統中眾多變數間的相互協調關係的變化。
④拓撲預測;將原始數據作曲線,在曲線上按定值尋找該定值發生的所有時點,並以該定值為框架構成時點數列,然後建立模型預測該定值所發生的時點。
關聯度
提出系統的關聯度分析方法,是對系統發展態勢的量化比較分析。
 關聯度
關聯度生成數列
分類
通過對原始數據的整理尋找數的規律,分為三類:
a、累加生成:通過數列間各時刻數據的依個累加得到新的數據與數列。累加前數列為原始數列,累加後為生成數列。
b、累減生成:前後兩個數據之差,累加生成的逆運算。累減生成可將累加生成還原成非生成數列。
c、映射生成:累加、累減以外的生成方式。
關係式
記x(0)為原始數列
x(0)=(x(0)(k)xk=1,2,…,n)=(x(0)⑴,x(0)⑵,…,x(0)(n))
記x⑴為生成數列
x⑴=(x⑴(k)xk=1,2,…,n)=(x⑴⑴,x⑴⑵,…,x⑴(n))
如果x(0) 與x⑴之間滿足下列關係,即
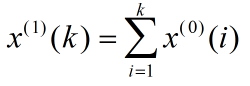 灰色預測
灰色預測稱為一次累加生成。
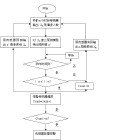
建模步驟
a、建模機理
b、 把原始數據加工成生成數;
c、 對殘差(模型計算值與實際值之差)修訂後,建立差分微分方程模型;
d、 基於關聯度收斂的分析;
e、 gm模型所得數據須經過逆生成還原後才能用。
f、採用“五步建模(系統定性分析、因素分析、初步量化、動態量化、最佳化)”法,建立一種差分微分方程模型gm(1,1)預測模型。
GM(1,1)模型
令 x(0)=(x⑴,x⑵,…,x(n))
作一次累加生成, k
x(k)= ∑x(m) 消除數據的隨機性和波動性
m=1
有 x=(x⑴,x⑵,…,x(n))
=(x⑴,x⑴+x⑵,…,x(n-1)+x(n))
x可建立白化方程:dx/dt+ax=u 即gm(1,1).
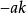 灰色預測
灰色預測該方程的解為: x(k+1)=(x⑴-u/a)exp(
)+u/a
其中:α稱為發展灰數;μ稱為內生控制灰數
GM(n,h)模型
1、殘差模型:若用原始經濟時間序列建立的GM(1,1)模型檢驗不合格或精度不理想時,要對建立的GM(1,1)模型進行殘差修正或提高模型的預測精度。修正的方法是建立GM(1,1)的殘差模型。
2、GM(n,h)模型:GM(n,h)模型是微分方程模型,可用於對描述對象作長期、連續、動態的反映。從原則上講,某一灰色系統無論內部機制如何,只要能將該系統原始表征量表示為時間序列x(0)(t),並有 x(0)(t)>0,即可用GM模型對系統進行描述。
特點介紹
對於一個模糊系統來說,傳統的預測方法就會失去作用。處理模糊預測問題的數學方法是模糊數學。模糊數學的基礎是模糊集合論,而模糊集合是普通集合的擴展。美國學者l.a.zadeh教授建立的模糊集合論,為模糊預測理論與方法的研究奠定了理論基礎。它用簡捷有力的方法處理複雜系統,在某種程度上彌補了經典數學與統計數學的不足。
套用信息
在預測套用上,如氣象預報、地震預報、病蟲害預報等,國內學者做出了許多有益的研究。
分析預測
混沌理論是這些年來長足發展的一門學科。混沌向世界規律運動的假定性提出挑戰。一方面,它告訴我們,宇宙遠比我們想得到的要怪異,它使許多傳統的科學方法受到懷疑。另一方面,混沌認為許多無規則的事物實際上可能是簡單規律的結果。混沌展現給我們的是一些新的規律。
混沌理論
遵從簡單規律的系統會以令人驚訝的複雜方式表現其行為。混沌是隱秘形式的秩序。混沌系統是指敏感地依賴於初始條件的內在變化系統,對外來變化的敏感性本身並不意味著混沌。混沌理論最令人興奮的是:一個非常簡單的決定論系統能夠產生異常複雜的輸出結果。給定一個簡單規則和初始條件,系統將產生複雜連續系列,這一點類似“無中生有”。
研究實例
美國科學家帕卡德和他的同事基於混沌和生物進化理論,藉助計算機,致力於用圖形來描述金融市場的混沌現象。帕卡德認為,世界上有大量不同的隨機現象,他所研究的是大體只需幾個變數就能描述系統行為的一種混沌現象。他試圖建立一種學習算法,對進化模型進行處理。而對於眾多的模型,帕卡德採用一種稱為遺傳算法的方法處理數據。它用類似生物繁殖中突變和雜交現象的方法來改變模型。這種方法的核心是,計算機不斷設定新的假設環境,從而使學習算法更具有適應性。認為一個好的學習算法不僅能建立適應模型,它還能時刻觀測數據的變化。所謂“學習算法”是一種特別的程式,他擅長對大量的、各種各樣的模型進行比較研究,找出哪個模型最適用於分析目前和未來的數據。
matla程式
%下面程式是灰色模型GM(1,1)程式二次擬合和等維新陳代謝改進預測程式,matlab6.5,使用本程式請註明,程式存儲為gm1.m%x = [5999,5903,5848,5700,7884];gm1(x); 測試數據 %二次擬合預測GM(1,1)模型function gmcal=gm1(x)ynyz = [124 113 154.1666667 240.0909091 224.3333333180.9 155.0909091 223.4166667 274.8333333 327.2533.33333333 92.5 57.5 382.5 101.333333360 69.75 62.66666667 136.6666667 202.7548.66666667 60.33333333 49.75 97.25 139.6666667111.4 98.18181818 118.75 168.8 243.5454545280.25 296.125 316.7777778 354 458.888888962.66666667 61.33333333 95.75 39.66666667 79223.1 205 235.3636364 303.8 355148.25 162 161.1666667 243 361.6650 522.8 629.7142857 915.6666667 1270.4780.3333333 726.6666667 924 1483.666667 1656.666667140 104.75 168.2 322 337.3333333292.6666667 344.3333333 454.3333333 416.3333333 943.5168.3333333 161.5 339 415.6666667 262.8290.3333333 270.25 317 548 494313.25 543 565.6666667 696.75 713308 328.4285714 379 432.1428571 521.83333331723.25 2060 2107 3643.666667 2416.6285.75 508 364.25 526.25 1142386.3333333 511.2 558.1666667 549.5 674.5348.2857143 412.3461538 502.96 694.88 747.564091.914286 4137.055556 4823.685714 6175.722222 7706.305556520 619 547.5 786 1142643.2352941 489.8095238 699.6666667 1133.25 1298.533333964.25 972 1220.809524 1408.565217 2286.909091210.6 234.8 304 428.5 544.857142979.75 110.6666667 107.2 283 415265.7333333 286.5714286 400.8125 415 425.68751873.285714 1623 1854.222222 2042.9 2665.5219.175 311.7 406.8928571 480.75 642.076923188.2 171 233 178.8 43833.33333333 183 223 269 733105.4 122.8125 130.5625 265.5 235.9444444134.4 104.3333333 247.25 293 385.1666667134.8 147 216.8571429 186.6666667 246.2533.33333333 44.25 116.75 96 54.6124.2 147 253 544 530.75114.5 109.5 150.5 219.3333333 300.857142957.66666667 51.6 89.6 166.6666667 253959.75 1120.25 2188 3439.5 44302461.857143 3007.714286 4046.571429 4783 6518.51871.2 1785.833333 3962.25 2489 72722396.833333 2322.714286 2950.142857 3408 4164.255154.25 5092 8304.333333 19573 13888.333332737 2675.428571 3227 3299.75 6860.41500.75 1813.857143 2180.166667 2722 3583.8571431417 1205.8 1414.5 1211.777778 1276.9255 278.6363636 305.1666667 386.4615385 596.076923120 33.33333333 100 132 217.5894 614.3333333 545 425.3333333 563285.8 308.4615385 443.75 511.2 710.1299.6 316 443 893.3333333 1023.666667240 278.5714286 361.6666667 704 848.650 61.33333333 100 273 841119.2 192.25 251 445 715159.6 142.4 225.5 396.3333333 357.533.33333333 63.66666667 71 177.5 137256.6666667 257 375.6666667 664.5 677215.1666667 194 329.6666667 361.1428571 385296.6666667 265 244.25 249 240.6666667292.5 355.75 415.75 407.2 574.4317.5 306.2 408.5 389.2 543.6315 409.4 504.8 472.6666667 711.484.33333333 116.5 153 128 253632 1013 855.3333333 1089.333333 1361.333333227.25 275.75 348 361 520225.3333333 260.4 264.5 305 426.5237.5 351.8 378 375.6666667 550.833333377 106.6 104.3333333 166.8 346.8148 443 189.3333333 379.5 604.5474.5 1182 1250 1019 1263.5];x = ynyz(72,:);sizexd2 = size(x,2);%求數組長度k=0;for y1=xk=k+1;if k>1x1(k)=x1(k-1)+x(k);%累加生成z1(k-1)=-0.5*(x1(k)+x1(k-1)); %z1維數減1,用於計算Byn1(k-1)=x(k);elsex1(k)=x(k);endend%x1,z1,k,yn1sizez1=size(z1,2);%size(yn1);z2 = z1';z3 = ones(1,sizez1)';YN = yn1'; %轉置%YNB=[z2 z3];au0=inv(B'*B)*B'*YN;au = au0';%B,au0,auafor = au⑴;ufor = au⑵;ua = au⑵./au⑴;%afor,ufor,ua %輸出預測的 a u 和 u/a的值constant1 = x⑴-ua;afor1 = -afor;x1t1 = 'x1(t+1)';estr = 'exp';tstr = 't';leftbra = '(';rightbra = ')';%constant1,afor1,x1t1,estr,tstr,leftbra,rightbrastrcat(x1t1,'=",num2str(constant1),estr,leftbra,num2str(afor1),tstr,rightbra,"+',leftbra,num2str(ua),rightbra)%輸出時間回響方程%******************************************************%二次擬合k2 = 0;for y2 = x1k2 = k2 + 1;if k2 > k elseze1(k2) = exp(-(k2-1)*afor); endend%ze1sizeze1 = size(ze1,2);z4 = ones(1,sizeze1)';G=[ze1' z4];X1 = x1';au20=inv(G'*G)*G'*X1;au2 = au20';%z4,X1,G,au20Aval = au2⑴;Bval = au2⑵;%Aval,Bval%輸出預測的 A,B的值strcat(x1t1,'=",num2str(Aval),estr,leftbra,num2str(afor1),tstr,rightbra,"+',leftbra,num2str(Bval),rightbra)%輸出時間回響方程nfinal = sizexd2-1 + 1;%決定預測的步驟數5 這個步驟可以通過函式傳入%nfinal = sizexd2 - 1 + 1;%預測的步驟數 1for k3=1:nfinalx3fcast(k3) = constant1*exp(afor1*k3)+ua;end%x3fcast%一次擬合累加值for k31=nfinal:-1:0if k31>1x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1);elseif k31>0x31fcast(k31+1) = x3fcast(k31)-x⑴;elsex31fcast(k31+1) = x⑴;endendendx31fcast%一次擬合預測值for k4=1:nfinalx4fcast(k4) = Aval*exp(afor1*k4)+Bval;end%x4fcastfor k41=nfinal:-1:0if k41>1x41fcast(k41+1) = x4fcast(k41)-x4fcast(k41-1);elseif k41>0x41fcast(k41+1) = x4fcast(k41)-x⑴;elsex41fcast(k41+1) = x⑴;endendendx41fcast,x%二次擬合預測值%***精度檢驗p C************//////////////////////////////////k5 = 0;for y5 = xk5 = k5 + 1;if k5 > sizexd2 elseerr1(k5) = x(k5) - x41fcast(k5); endend%err1%絕對誤差xavg = mean(x);%xavg%x平均值err1avg = mean(err1);%err1avg%err1平均值k5 = 0;s1total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2 elses1total = s1total + (x(k5) - xavg)^2; endends1suqare = s1total ./ sizexd2;s1sqrt = sqrt(s1suqare);%s1suqare,s1sqrt%s1suqare 殘差數列x的方差 s1sqrt 為x方差的平方根S1k5 = 0;s2total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2 elses2total = s2total + (err1(k5) - err1avg)^2; endends2suqare = s2total ./ sizexd2;%s2suqare 殘差數列err1的方差S2Cval = sqrt(s2suqare ./ s1suqare);Cval%nnn = 0.6745 * s1sqrt%Cval C檢驗值k5 = 0;pnum = 0 ;for y5 = xk5 = k5 + 1;if abs(err1(k5) - err1avg) < 0.6745 * s1sqrtpnum = pnum + 1;%ppp = abs(err1(k5) - err1avg) elseendendpval = pnum ./ sizexd2;pval%p檢驗值%arr1 = x41fcast(1:6)%預測結果為區間範圍 預測步長和數據長度可調整程式參數進行改進