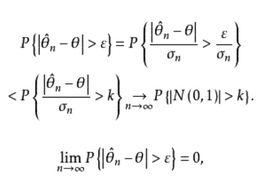基本介紹
 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計相合性反映了當時估計量的優良性質,但由於參數的相合估計可以不止一個,它們之間的差異可以用估計量的漸近分布的漸近方差反映出來。
 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計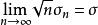 漸近正態估計
漸近正態估計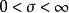 漸近正態估計
漸近正態估計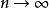 漸近正態估計
漸近正態估計定義 設是的估計量,如果存在一串,滿足,其中,使得當時,有
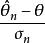 漸近正態估計
漸近正態估計的分布收斂於N(0,1)
 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計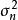 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計則稱是的 漸近正態估計,稱為的 漸近方差。
 漸近正態估計
漸近正態估計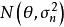 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計當樣本容量n足夠大時,對於一個漸近正態估計,可以用作為的近似分布,從而可以對進行區間估計。
容易證明,漸近正態估計一定是相合估計,但不一定是強相合估計。
 漸近正態估計
漸近正態估計對某個待估參數,如果存在著漸近正態估計,這樣的估計可能並不唯一。因此漸近方差的大小就可以作為比較這些估計優劣的一個準則。
相關概念與定理
 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計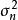 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計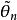 漸近正態估計
漸近正態估計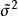 漸近正態估計
漸近正態估計最優漸近正態估計設為待估參數的一個漸近正態估計,漸近方差為,若對的任意漸近正態估計,漸近方差記內、有
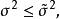 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計則稱為的 最優漸近正態估計(the best asymptotically normal estimate) 。
定理 漸近正態估計一定是相合估計。
 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計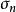 漸近正態估計
漸近正態估計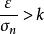 漸近正態估計
漸近正態估計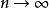 漸近正態估計
漸近正態估計證明: 設是的漸近正態估計,由定義,對任意及k>0,當n充分大時必須充分小,因此,故當時有
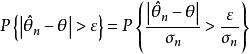 漸近正態估計
漸近正態估計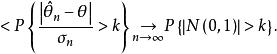 漸近正態估計
漸近正態估計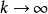 漸近正態估計
漸近正態估計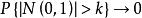 漸近正態估計
漸近正態估計由k的任意性,令,由於,因此
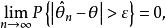 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計 漸近正態估計
漸近正態估計即是的相合估計 。
例題解析
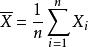 漸近正態估計
漸近正態估計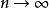 漸近正態估計
漸近正態估計例1 設X~B(1,p)(二項分布),(X,X,…,X)是X的樣本,p的一個估計量是,由中心極限定理,當時有
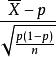 漸近正態估計
漸近正態估計的漸近分布為N(0,1),
 漸近正態估計
漸近正態估計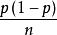 漸近正態估計
漸近正態估計故是p的漸近正態估計,漸近方差為。