地震和彈簧滑塊模型
假定地震是由斷層的滑動造成的,而一條大斷層可以分成許多段(fragmentation),當一段斷層滑動時發生小地震;多段斷層同時滑動則產生大地震,而且各段斷層之間存在著彈性耦合作用。Burridge和Knopoff(1967)用圖1的彈簧滑塊模型來描述地震的活動特徵,圖1中每個滑塊代表大斷層上的一段斷層,滑塊,之間以彈簧連線,所有的滑塊又都以彈簧連到一個以常速度v運動的巨大板塊上,當作用於一塊滑塊上的力小於摩擦力時,滑塊仿佛被黏在滑動面上,靜止不動。一旦作用力達到靜摩擦力時,該滑塊就會發生運動,由於當時計算機能力的限制,最初模型中的滑塊數目不超過10。
20多年後,由於計算機能力的極大增強,Carlson和Langer(1989)已將模型中的滑塊數量增加到200個以上,Levi(1990)利用彈簧滑塊模型,模擬出地震活動的許多統計規律。
地震活動性最重要的統計規律是Gutenberg—Richter關係,簡稱為G—R關係,即:
lgf(m)=c-bm,(1)
其中,f(m)為一段時間中發生震級等於或大於m的地震頻度;b和c是常數;m是地震的震級,它是地震矩的對數,若將地震震級m和地震矩M的關係寫作:
m=dlgM,
式中,d也是一個常數,則可得
f(m)=1/M ,
其中,α=bd是個常數。因此,式(1)表示大小地震的頻度和震級(或地震矩)之間存在著冪指數關係,這是一種典型的分形(陳顆,1988)。式(1)自40年代發現以來,它對於變化達10個數量級的地震活動性都適用,這表明,大小地震遵循著相同的冪律,而且,大小地震的產生受著一種與尺度無關的機理控制。
Carlson等定義,在彈簧滑塊模型中所有同時滑動的滑塊滑動距離之和為該次滑動事件的“矩”,這個矩的對數即為滑動事件的震級,他滑動事件數目N(m)的結果與G—R關係完全一致,都是一種分形關係。彈簧滑動模型廣泛地用於地震活動性的研究中(張國民等,1993)。
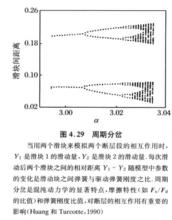 圖2
圖2彈簧滑塊模型還可以用來研究岩石摩擦特性對斷層段相互作用的影響,Huang和Turcotte(1990)研究了兩個滑塊的運動情況,若給定滑塊與滑動面之間的靜摩擦力F是動摩擦力F的1.25倍(即F/F=1.25),同時滑塊2的靜摩擦力是滑塊1的2.25倍,則兩個滑塊之間的相對距離y一y隨參數α=K/K的變化如圖2所示,當α=3.02時,y一y可以取兩個值中的一個,或者是0.085,或者是0.175.當α增加到3.03時,這時y一y有4個可能值,即出現了分岔現象,隨著α的進一步增加,分岔也越來越多。分岔是混沌動力學的顯著特點,岩石的摩擦特性在決定如地震、滑坡之類的失穩運動時,起著十分重要的作用 。
用滑塊模型對衝擊地壓的研究
(1)衝擊地壓的發生是頂底板瞬時加、卸載,煤層瞬時破壞的過程;而粘滑是應力瞬時松馳和增加的過程。粘滑的產生表明了正應力與剪應力的關係。實際衝擊地壓發生在斷層、煤層變薄帶、煤層頂底板附近。剪下強度相對較低和較大的高水平構造應力環境是煤岩系統滑移失穩的客觀條件,因此,可以用單狀態變數本構模型描述衝擊地壓的動力學行為。
(2)粘滑是煤岩主要力學特性的一種表現形式,而衝擊地壓則是煤岩滿足剪下強度準則、以突然滑動並在滑動過程中伴有動能釋放的動力過程。粘滑的產生不僅與摩擦特性有關,而且與載入系統的特性有關,衝擊地壓是煤岩系統的動力失穩過程,用粘滑機制可以很好解釋衝擊地壓發生機理。
(3)對單變數本構模型,彈簧的剛度K,β對系統的動力學行為和狀態變數的演化行為貢獻較大,而系統動力學行為和狀態變數演化行為對φ,f初值的敏感性相對較低。由於單變數本構模型的局限性,它不能很好的模擬系統的粘滑特性,雙狀態變數本構模型很好地解決了這個問題 。