概述
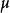湯川理論 湯川理論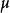
湯川理論帶電粒子之間的力是通過電磁場的中間作用的，而電磁場又有時顯出粒子性。電磁場的量子就是光子。電磁場理論的成功向人們提示了是否對核力也可以建立一種場的理論。1935年湯川秀樹提出一種理論，說核子之間也通過一種場起作用，而這種場的量子是一種具有靜質量的粒子，其靜質量大約是電子質量的200倍。1936年在宇宙線中發現了一種粒子，後來稱為 子，其質量正是稍大於電子質量的200倍。當時以為湯川所說的粒子由此已經證實。後來逐漸搞清楚了 子不符合湯川理論的要求。到了1947年另一種粒子被鮑威爾等發現，其質量是電子質量的273倍，稱為 介子，這才是湯川理論中的粒子。
基本原理
正如帶電粒子之間的電磁場可以用勢函式來描述，對核子之間的核力場也可以推得適當的勢函式，並從而可以估計核力場的量子應有的靜質量。下面我們對靜介子場進行一些推算。
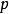湯川理論
湯川理論一個具有靜質量 和動量 的自由粒子的哈密頓函式按照相對論是：
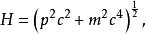湯川理論平方後成為：
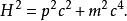湯川理論
湯川理論
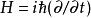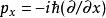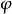湯川理論
湯川理論用量子力學的算符 ， 等代入，使運算於勢函式 ，即得：
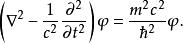湯川理論 湯川理論此式稱克萊恩-戈登方程，適用於自旋為0的自由粒子。 介子符合這個要求。
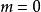湯川理論
湯川理論如果令上式中的 ，這公式就成為熟悉的電磁場公式。對靜電場，式中對時間微商一項又等於零。如果在坐標的原點上有一固定的電荷 ，靜電場的公式可列為：
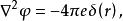湯川理論式中，
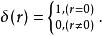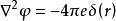湯川理論
湯川理論其中， 式子的解是：
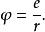湯川理論
湯川理論 湯川理論如果離原點為 的地方另有電荷 ，則兩電荷的勢能是：
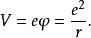湯川理論
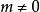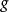湯川理論
湯川理論相似的情況是靜介子場，此時 。仍設坐標的原點上有一核子，它帶有相當於電荷的代表核力強度的量 ，那么勢函式的方程是：
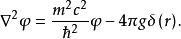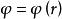湯川理論
湯川理論設 ，是球形對稱的，上式可解出：
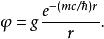湯川理論 湯川理論如果離原點為 的地方有另一核子，兩核子之間的勢能是：
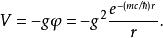湯川理論這個勢能是負的，因為作用力是吸引力。
湯川理論 湯川理論
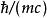湯川理論這個勢函式隨 的增加急劇地趨於零，代表了短程力。當 大於之術中的常數 時，力就很小，所以這個常數值就代表力程的數量級。另一方面，力程的數量級應該與原子核大小相仿。這樣，
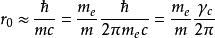湯川理論
湯川理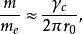論
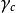湯川理論式中的 是康普頓波長，把這些數值代入，就得：
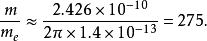湯川理論 湯川理論這同 介子質量的實驗值很接近。
