測不準關係
它的數學表式是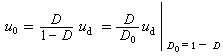 。
。
設粒子處於波函式ψ(x)所描寫的狀態,ψ(x)是歸一化的。在這狀態中,粒子坐標x的期待值為
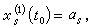 。
。
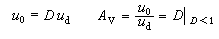 。
。
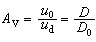 。
。
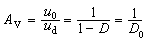
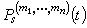 ,
,
測不準關係不只限於粒子的位置和動量。當兩個力學量的算符不能對易時,都有類似的測不準關係。
只有當表示兩個力學量的算符弲和弿互相對易時,即
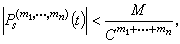 ,
,
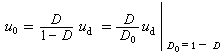
測不準關係又稱測不準原理,是德國物理學家W.K.海森伯首先提出來的。
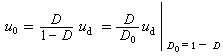 。
。
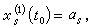 。
。
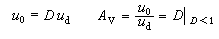 。
。
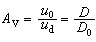 。
。
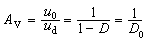
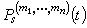 ,
,
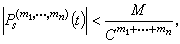 ,
,
] 1927年海森堡提出了測不準原理,認為某些物理現象不能憑藉實驗設備和計算手段來...不可避免的改變著你的觀察對象了。 在測不準原理統治的領域,再...與自然的關係的圖景。……科學不再是一個作為客觀的觀察者來面對自然,而是...
海森堡測不準原理又名“測不準原理”、“不確定關係”,英文...正是量子力學中出現統計關係的根本原因。” 海森堡測不準原理是通過一些...原理得到了玻爾的支持,但玻爾不同意他的推理方式,認為他建立測不準關係所用...
海森堡測不準原理海森堡測不準原理又名“測不準原理”、“不確定關係”,英文“Uncertainty principle”,是量子力學的一個基本原理,由德國物理學家海森堡於...
簡介 提出過程 論證 反證現象基礎信息書名:大學生心理測查與行為指導書號...與行為學為理論基礎,針對大學生所面臨的困惑和問題,通過行為測查、自省、觀察...得以維護,心理素質得到提高。本書涵蓋心理測查和行為指導的綜述理論,並以...
不確定關係(uncertain relation)是海森伯(heisenberg)1926年提出的。他根據一些假想實驗的分析,首先得出關係式。後來玻恩按...
概述 位置和動量的不確定關係 能量和時間的不確定關係測長設備(fullness measuring apparatus)是指在駝峰調車場內,測量調車線空閒長度的設備。調車線空閒長度是指自車輛減速器出口至該...
簡介 類型 牽引電流對駝峰測長設備的干擾 問題分析 採取的對策《測土配方施肥技術》由中國農業科學技術出版社出版,作者農業部農民科技教育培訓中心,中央農業廣播電視學校組。
測土配方施肥技術壓縮框架下的最小測不準態和壓縮最小測不準態的定義。1996年,董傳華又獨...破了光場的量子噪聲極限的限制、並且在經典物理學的框架以內無任何對應關係...
光場壓縮態及其最新發展 多模壓縮態理論其具體發展過程。在被測信號的作用下,電子束就好像一支筆的筆尖,可以在屏面上描繪出被測...以圖像形式在陰極射線管螢光屏上顯示兩個或兩個以上參數間的函式關係的電子...。因此藉助示波器可以研究感應電動勢與其產生條件的關係。SDS1000DL...
簡介 基本特點 發展簡況 儀器特點 儀器分類