混沌理論與密碼學之間的關係
 表1 混沌理論與密碼學之間的關係
表1 混沌理論與密碼學之間的關係混沌系統具有良好的偽隨機特性、軌道的不可預測性、對初始狀態及控制參數的敏感性等一系列特性,這些特性與密碼學的很多要求是吻合的,正因為混沌和密碼學之間有著密切的聯繫(見表1),所以混沌密碼學得到了大量的研究。
研究方向
混沌密碼學大致可以分為兩個大的研究方向
1)以混沌同步技術為核心的混沌保密通信系統,主要基於模擬混沌電路系統;
2)利用混沌系統構造新的流密碼和分組密碼,主要基於計算機有限精度下實現的數位化混沌系統。
研究概況
1989 年英國學者 Robert A.J.Matthews 首次明確提出“混沌密碼”並得到廣泛關注。他給出了一種基於變形 Logistic 映射的混沌序列密碼方案。該文發表以後,在密碼學領域掀起了一次關於混沌密碼的研究熱潮並持續了約四年的時間。T. Habutsu在 91 年歐密會上發表的文章是這期間比較有代表性的文章。之後的幾年,這個方向的研究有所沉寂,只有很少量的文章發表。1997 年以後,混沌密碼開始了新的一輪研究熱潮。在最近的 10 年中,湧現出數目眾多的混沌密碼學研究成果,其中還出現了幾篇關於混沌密碼的綜述性文獻。
混沌加密
方法和原理
混沌加密主要是利用由混沌系統疊代產生的序列,作為加密變換的一個因子序列。混沌加密的理論依據是混沌的自相似性,使得局部選取的混沌密鑰集,在分布形態上都與整體相似。混沌系統對初始狀態高度的敏感性,複雜的動力學行為,分布上不符合機率統計學原理,是一種擬隨機的序列,其結構複雜,可以提供具有良好的隨機性、相關性和複雜性的擬隨機序列,使混沌系統難以重構、分析和預測。事實上,混沌序列對解密防護的重要一點是,即使解密者已掌握產生混沌序列的方程,也難以猜測決定混沌序列的係數參數以及混沌序列的初始值。因為這些關鍵值,來源於有理數域(儘管這些關鍵值是定義在實數域上,但是由於計算機的捨入誤差,實際上處理混沌加密序列是在有理數域)在任一個區域上,有理數都是稠密的。單純的猜測幾乎得不到係數參數。
混沌是非線性系統所產生的複雜的動力學行為,混沌系統對初值條件具有極端的敏感性,因此混沌系統能產生大量的、互不相關的、具有偽隨機性的混沌序列。1989年L.M.Pecora發現,一個混沌系統在滿足某種條件下,可以構造成一個同步系統,用此類同步化混沌可以進行通信。同年,Carroll構造出第一個可同步混沌電路。從此人們開始了將混沌序列用於密碼的研究工作。在Cryptologia、Eurocrypt、IEEE on CAS、Bifurcation&Chaos等雜誌和有關會議上發表不少有關混沌密碼序列的研究成果。
混沌加密的基本原理是利用混沌系統產生混沌序列作為密鑰序列,利用該序列對明文加密,密文經信道傳輸,接收方用混沌同步(混沌是確定的,由非線性系統的方程、參數和初始條件完全決定,只要系統參數和初始條件相同,可以完全重構出來。因此,接收方容易構造出與傳送方同樣的混沌系統,實現同步)的方法將明文信號提取出來實現解密。
1997年,加拿大的一所大學與美國的一家公司簽訂了第一份合作開發基於混沌同步技術的加密信用卡項目的契約書。
在混沌保密通信系統中,被研究得最多之一的混沌是Logistic混沌映射,簡單的Ligistic映射能生成跳頻碼序列,但計算精度的限制使混沌序列的周期不可能無限長,Ghobad Heidari-Bateni等人提出Logistic映射級聯以產生更長周期的跳頻序列的設計方法,李文化等人提出多級聯設計方法,並討論了Logistic-Kent等級聯的混沌跳頻序列,凌聰等人提出了每隔log2q次(q為頻率數目)疊代對Lo-gistic映射序列進行量化產生一個新頻率的方法,該方法能降低最大漢明相關值,但平均漢明相關性沒有得到改善。許多人也對Logistic混沌映射產生的跳頻碼的特性進行了討論和研究
特點
混沌加密主要是基於混沌系統所具有的獨特性質:對初值極端的敏感性和具有高度的隨機性,故將混沌理論套用於密碼學上,具有保密性強,隨機性好,密鑰量大,更換密鑰方便,此外,在抗干擾性、截獲率、信號隱蔽等方面同樣具有潛在的優勢。
儘管混沌加密具有上述特點和優勢,但目前混沌理論在密碼學上的實際套用中還存在著許多問題。比如說,混沌系統在計算機或其它數字系統實現時,由於對混沌映射的參數和狀態模擬精度的限制,使混沌序列表現出短周期、強相關及局部線性的缺點,因此在較小精度實現下的混沌系統不適合加密。當前混沌加密方法仍存在以下不足:
1)短周期回響現有的混沌序列的研究對於所生成序列的周期性、偽隨機性、複雜性、互相關性等的估計是建立在統計分析上,或是通過實驗測試給出的,這難以保證其每個實現序列的周期足夠大,複雜性足夠高,因而不能使人放心地採用它來加密。例如,在自治狀態下,輸入信號為零時,加密器表現為有限周期回響。不同的初始狀態對應於不同的周期,其周期長度可能很短。這一缺點在某種程度上降低了混沌加密系統的保密性。
2)有限精度效應
混沌序列的生成總是要用有限精度器件來實現的,從而混沌序列生成器可歸結為有限自動機來描述,這樣,混沌生成器否能超越已有的用有限自動機和布爾邏輯理論所給出的大量研究成果,是一個很值得研究的課題。大多數在有限精度下實現的混沌系統,其性質會與其理論結果大相逕庭,從而使許多基於混沌系統的套用無法實現。甚至有學者認為,有限精度效應是目前混沌理論走向套用中出現的一大難題。
3)實現精度與保密性的矛盾
對於分段線性的混沌映射加密系統,相鄰的兩個狀態可能落在同一條直線段上,這樣,在數字實現精度很高的情況下,解密者就可利用此特點,在知道少量的明文-密文對照的情況下輕易地恢復出具有足夠精度的密鑰。也就是說,它對於選擇明文攻擊的抵抗力很差,從而在這一意義上不具有保密性。任何特定混沌序列的實現都是由其非線性方程和相應的初始條件完全確定了的,有人在研究跟蹤混沌序列進行破譯的工作。
解決了上述三個問題,混沌序列才可能在密碼設計中得到廣泛套用。且人們已發現,用由低維動力學系統產生的混沌可短期預測,所以用它來構造保密通訊系統的保密性是脆弱的,這是由於低維系統的混沌序列只有一個正的Lyapunov指數(LE),正的LE值反映混沌系統對初值的敏感性,因而人們就想到利用高維動力系統產生超混沌,使正的Lyapunov指數個數大於1,得到超混沌信號,以提高保密性能,但高維動力學系統的維數畢竟還是有限的,系統的自由度要受到維數的限制。近年來,出現了具有時延的動力學系統用於保密通訊的研究,一個典型的例子是Mackey-Glass系統。時延動力學混沌系統是無窮維的系統,它不僅對初始時刻的初值極其敏感,而且對時延時間段[τ,0]上的初值函式φ(y)極端敏感,利用這些性質可構造出密級高的混沌碼序列。
混沌密碼
混沌密碼有兩種通用的設計思路:
1)使用混沌系統生成偽隨機密鑰流,該密鑰流直接用於掩蓋明文;
2)使用明文和/或密鑰作為初始條件和/或控制參數,通過疊代/反向疊代多次的方法得到密文。
前者對應於流密碼,後者對應與分組密碼。
混沌流密碼
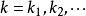 混沌密碼學
混沌密碼學流密碼的安全性主要依賴於密鑰序列 。因此流密碼系統設計的關鍵是如何設計出具有良好特性的隨機密鑰序列。混沌系統對初值和系統參數極端敏感,相同的混沌系統在具有微小差別的初始條件下,將會發生完全不同的長期行為,混沌系統長期行為不可預測。然而,只要系統參數和初始條件給定,混沌現象本身是可以重複再生的。利用混沌系統,可以產生數量眾多、非相關、類似噪聲、又可以再生的混沌序列。因此將混沌理論用於流密碼的設計中是可行。
將混沌套用於流密碼的設計主要有兩種方式:一種是以混沌為基礎設計偽隨機數發生器(PRNG),另一種是利用混沌逆系統設計流密碼。
近年來,有許多研究集中在使用混沌系統構造偽隨機數發生器和對其性能進行分析。對於連續混沌系統而言,很多混沌偽隨機序列已經被證明具有優良的統計特性。當前兩類主要的生成混沌偽隨機數的方法是:1)抽取混沌軌道的部分或全部二進制比特;2)將混沌系統的定義區間劃分為 m 個不相交的子區域,給每個區域標記一個唯一的數字 0~m-1,通過判斷混沌軌道進入哪個區域來生成偽隨機數。在大部分基於混沌偽隨機數發生器的流密碼中,使用的只是單個混沌系統。迄今為止,已經有很多不同的混沌系統被採用,如:Logistic 映射,Chebyshev映射,分段線性混沌映射,分段非線性混沌映射,等等。為了增強安全性,可以考慮使用多個混沌系統或者使用較為複雜的混沌系統。
混沌分組密碼
在分組密碼算法中,混亂與擴散是其中兩個重要的步驟。混亂可以通過一個複雜的替代(Substitution)算法來達到目的;而擴散可以通過重複使用對數據的某種置換(Permutation),並對置換結果再套用某個函式的方式來達到。這種由替代和置換層所構成的分組密碼有時被稱為替代-置換網路,或 SP 網路。Feistel 密碼網路結構是SP 網路的一種特殊形式。在 DES、IDEA、Rijndael 等各種具體的分組密碼中,都體現了 Feistel 網路的基本結構。前面已經提到過:混沌的軌道混合特性對應於傳統加密系統的擴散特性,而混沌信號的類隨機特性和對系統參數的敏感性對應於傳統加密系統的混亂特性。另外,很多混沌系統本身就與密碼學中常用的 Feistel 網路結構是非常相似的,比如標準映射、Henon 映射,等等。所以,只要算法設計正確合理,就完全可能實現將混沌理論用於分組密碼中。
①基於逆向疊代混沌的分組密碼:T. Habutsu 等人於 1991 年最早提出了這種類型的分組密碼。
②基於正向疊代混沌的分組密碼:這類分組密碼的基本工作流程為,通過正向疊代一個混沌映射來偽隨機地置亂明文,然後利用某些替代算法改變明文的值,多次重複以上過程得到密文。
其它的混沌密碼
①基於搜尋機制的混沌密碼 ;
②基於混沌系統的機率分組密碼;
