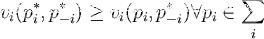混合策略納什均衡

混合策略納什均衡：在n個參與人的博弈G=S1 ,... Sn ; u1 ,...un中，混合策略組合構成一個納什均衡，如果對於所有的i=1，2...，n下式成立： 也就是說，如果一個策略組合使任何一個參與人的策略都是相對於其他參與人的策略的最佳策略，這個策略就構成一個納什均衡，不管這個策略是混合策略還是純策略。 混合策略納什均衡是面對其他博弈者選擇的不確定性的一個理性對策，其主要特徵是作為混合策略一部分的每一個純策略有相同的期望值，否則，一個博弈者會選擇那個期望值最高的策略而排除所有其他策略，這意味著原初的狀態不是一個均衡。

概要

在博弈G={S1,S2……Sn；U1,U2……Un}中第i個博弈方策略空間為Si={Si1……Sik}則博弈方以機率分布Pi=(Pi……Pik)隨機在k個可選策略中選的的策略稱為一個混合策略納什均衡。

定理

矩陣博弈A中，A=（aij）,混合策略納什均衡 點存在的充分必要條件為：v1=max min E(x,y)=min max E(x,y)=v2

原理

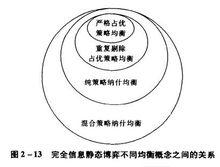
嚴格占優策略均衡、重複剔除的占優策略均衡、純策略納什均衡和 混合策略納什均衡。一般將上述四種均衡統稱為納什均衡。

在這四種均衡概念中每種均衡依次是前一種均衡的擴展。前一種均衡是後一種均衡的特例。嚴格占優策略均衡是重複剔除的占優策略均衡的特例；重複剔除的占優策略均衡是純策略納什均衡的特例；純策略納什均衡是混合策略納什均衡的特例。

如果將完全信息靜態博弈中存在某種均衡的所有博弈定義為一個集合，那么就存在前一種均衡的博弈集合是後一種均衡的博弈集合的子集。完全信息靜態博弈四種均衡概念之間的關係可以用圖2—13表示。

混合策略納什均衡

實現

1、最大化收益法：即最大化各個參與人的效用函式。

2、收益相等法：根據前面分析的猜硬幣博弈中參與人的策略的思路，每個參與人的混合策略都使其餘參與人的任何純策略的期望收益相等，因此，解混合策略納什均衡可以令參與人的各個純策略收益相等，構成方程組求解。