理論描述
 消費者均衡
消費者均衡基數效用理論認為,在消費者收入與商品價格既定時,其最大滿足受支付能力的制約。如果消費者將其收入(R)全部都用於支出,那么他所購買的各種消費品的數量還必須符合一個條件,即預算支出等於收入總額(R=PAQA+PBQB+PcQc+…其中P表示商品價格,Q表示商品數量)。當消費者的支出既等於預算支出,又使每一種支出所得到的各種商品邊際效用相等時,該消費者在其收入許可的條件下,已得到最大的滿足,他再也不能從改變消費品構成與數量中得到更多的效用。該消費者不再改變其消費品構成與數量,這叫做消費者均衡。
序數效用中的描述
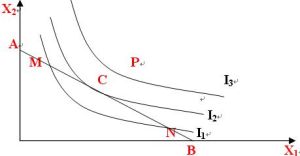
序數效用理論認為,假設消費者收入一定,並全部用於消費,同時假定商品X與Y的價格不變,那么消費者可能消費兩種商品的各種組合必等於消費者收入,在平面坐標上會形成一條線ABAB線上在任一點,都是消費者收入(或預算)在許可的條件下兩種商品可能的組合,所以AB線被稱為消費者可能線。AB線上方的任一點,都表示消費者購買力不及;AB線下方的任一點,表明消費者沒有取得他能夠取得的商品量;AB線上的各點則是消費者在商品價格既定條件下,以其收入可購得的兩種商品的各種量的組合。消費者為其收入許可條件下選擇能獲得最大滿足的商品組合,應將其無差異曲線圖(見序數效用理論)與消費可能線置於同一圖中,由無差異曲線與消費可能線的切點來決定其應取的商品組合,消費者既然在其無差異曲線與消費可能線的切點所示的商品組合中可以取得最大的滿足,就不再改變其消費品構成,所以被稱為消費者均衡。這一分析與基數效用分析完全一致。
消費者均衡的必要條件
在一定的收入和價格條件下,購買各種物品使總效用達到極大值或者使消費者得到最大的滿足的必要條件是:消費者所購買的各種物品的邊際效用之比等於它們的價格之比。
假設條件
 消費者均衡
消費者均衡這就是說,消費者對各種物品效用的評價是既定的,不會發生變動。也就是消費者在購買物品時,對各種物品購買因需要程度不同,排列的順序是固定不變的。比如一個消費者到商店中去買鹽、電池和點心,在去商店之前,對商品購買的排列順序是鹽、電池、點心,這一排列順序到商店後也不會發生改變。這就是說先花第一元錢購買商品時,買鹽在消費者心目中的邊際效用最大,電池次之,點心排在最後。
2、消費者的收入既定
由於貨幣收入是有限的,貨幣可以購買一切物品,所以貨幣的邊際效用不存在遞減問題。因為收入有限,需要用貨幣購買的物品很多,但不可能全部都買,只能買自己認為最重要的幾種。因為每一元貨幣的功能都是一樣的,在購買各種商品時最後多花的每一元錢都應該為自己增加同樣的滿足程度,否則消費者就會放棄不符合這一條件的購買量組合,而選擇自己認為更合適的購買量組合。
3、物品的價格既定
由於物品價格既定,消費者就要考慮如何把有限的收入分配於各種物品的購買與消費上,以獲得最大效用。由於收入固定,物品價格相對不變,消費者用有限的收入能夠購買的商品所帶來的最大的滿足程度也是可以計量的。因為滿足程度可以比較,所以對於商品的不同購買量組合所帶來的總效用可以進行主觀上的分析評價。
4、均衡位置
無差異曲線代表的是消費者對不同商品組合的主觀態度,而預算線約束則顯示了消費者有支付能力的商品消費的客觀條件,將兩者放在一起,就能決定消費者的最後選擇。把無差異曲線與預算線合在一個圖上,那么,預算線必定與無差異曲線中的一條切於一點,在這個切點上就實現了消費者均衡。
限制條件
1、兩種商品消費均衡的文字表述消費者均衡實現的限制條件是:消費者用全部收入所購買的各種物品所帶來的邊際效用,與為購買這些物品所支付的價格的比例相等,或者說每單位貨幣所得到的邊際效用都相等。
2、兩種商品消費均衡數學公式
假設消費者的收入為M,消費者購買並消費X與Y兩種物品,X與Y的價格為Px與Py,所購買的X與Y的數量分別為Qx與Qy,X與Y所帶來的邊際效用為MUx與MUy,每1單位貨幣的邊際效用為MUm,這樣,消費者均衡的條件可寫為:
Px*Qx+Py*Qy=M(1)
MUx/Px=MUy/Py=MUm(2)
上述(1)式是消費者均衡的收入約束條件,說明收入是既定的,購買X與Y物品的支出不能超過收入總額M,也不能小於收入總額M。超過收入的購買是無法實現的,而小於收入的購買也達不到既定收入時的效用最大化。(2)式是消費者均衡實現的評價條件,即所購買的X與Y物品帶來的邊際效用與其價格之比相等,也就是說,每一單位貨幣不論用購買X還是Y商品,所得到的邊際效用都相等。
3、多種商品消費均衡數學公式
如果消費者所消費的不是兩種物品,而是多種物品,設各種物品的價格為P1,P2,P3,……Pn,購買量為Q1,Q2,Q3,……Qn,各種物品的邊際效用為MU1,mu2,……MUn,則可以把消費者均衡實現的條件寫為:
P1*Q1+P2*Q2……+Pn*Qn=M(1)
MU1/P1=MU2/P2=…MUn/Pn(2)
4、實例分析
(1)、例題:假設某個消費者準備購買X與Y兩種商品,已知兩種商品的價格分別為Px=10,Py=20元,該消費者的收入為100元,並將其全部用於購買X和Y兩種商品。兩種商品的邊際效用MUx和MUy如表,此消費者應該購買多少X,多少Y才能使得總效用最大?
(2)、分析過程
根據收入約束條件:100=10X+20Y的限制,該消費者能夠購買的X和Y這兩種商品的所有整數的組合是有限的。依據給定的條件,該消費者購買這兩種商品不同數量的組合,及相應的MUx/Px與MUy/Py和總效用,如表3所示。根據表3所列出的資料,運用實現消費均衡的限制條件,就可以確定該消費者實現效用最大化的兩種商品的購買量組合比例。
由表2可以看出:只有在Qx=4,Qy=3的購買量組合時,才既符合收入條件的限制,又符合MUx/Px=MUy/Py的要求。此時,該消費者購買X商品所帶來的總效用為14,購買Y商品所帶來的總效用為15,購買X商品與Y商品所帶來的總效用為14+15=29。也就是實現了消費均衡。