歷史
人的支付函式類型是不清楚的。如果一些局中人不知道另一些局中人的支付函式,或支付函式不是共同知識,局中人就不知道他在與誰博弈,博弈的規則是沒有定義的。因而在1967年以前,博弈論專家認為此時博弈的結構特徵是不確定的,無法進行分析。海薩尼提出了一種處理不完全信息博弈的方法,即引入一個虛擬的局中人——“自然”。自然首先行動,它決定每個局中人的特徵。每個局中人知道自己的特徵,但不知道別的局中人特徵。這種方法將不完全信息靜態博弈變成一個兩階段動態博弈,第一個階段是自然N的行動選擇,第二階段是除N外的局中人的靜態博弈。這種轉換被稱為“海薩尼轉換”,這個轉換把“不完全信息”轉變成為完全但不完美信息,從而可以用分析完全信息博弈的方法進行分析。
“不完美信息”指的是,“自然”作出了它的選擇,但其他參與人並不知道它的具體選擇是什麼,僅知道各種選擇的機率分布。
1967年,海薩尼(John Harsanyi),指出所有老定義下具有不完全信息的博弈都可以在不改變其精髓的情況下被重新模型化為一個完全但不完美的信息博弈,這一切只需要添加一個由自然在不同規則集合中進行選擇的初始行動即可。在老的定義中,博弈論學家常指出不完全信息博弈是不可分析的,而海薩尼的創見使得這一切有所改變。老的定義是這樣描述的:在完全信息博弈中,全體參與人都知道博弈的規則,否則這一博弈就是一個不完全信息博弈。
儘管海薩尼未指出老的定義是有問題的,但事實上人們的觀點已經發生了變化,認為在原有定義中,被轉換後的博弈才是不完全信息博弈。在博弈中,其中有參與人也許對博弈的支付並不十分清楚,但對支付還是有一定的了解的。一般情況下,採用主觀概分布來表示信息。也就是基於機率對進行分組構建各種博弈支付,可以形成一個特定的支付集合。比如甲與乙選擇策略時,可以這樣考慮,甲選擇某一種策略時,乙選擇策略有幾種,乙的這些策略按發生的機率進行分組。通常構建一個博弈樹就可以較好地表達這一切。海薩尼教義的觀點關鍵在於假定所有的參與人都是有共同的認識,對於策略採取發生的機率是一個共同知識。隱含的意思也就是:參與人對於自己的猜測至少是少許公開了的。在對一個博弈的信息結構進行劃分的時候,並不試圖決定參與人能從其它參與人的行動中推斷出些什麼東西。先驗機率是作為博弈規則的一部分存在,因此,一個參與人必須是持有關於其它參與人類型的先驗信念,同時,在觀察到他們的行動後,就要假定他們遵循著均衡的行為,然後更新自己的信念。
實踐操作
套用
按照海薩尼的方法,所有參與人的真實類型都是給定的。其他參與人雖然不清楚某一參與人的真實類型,但知道這些可能出現的類型的分布機率,而且這種機率是公共知識。用上例來說,公共知識不僅意味著B企業知道A企業高阻撓成本與低阻撓成本的分布機率,而且意味著A也清楚B知道這一機率。通過海薩尼轉換,不完全信息博弈變成了完全但不完美信息博弈(games of complete but imperfect information)。這裡的不完美信息,就是指其他參與人只知道某一參與人某些方面類型的分布機率,而不知道該參與人在這些方面的真實類型。在上述轉換的基礎上,海薩尼提出了貝葉斯納什均衡(Bayesian Nash equilibrium)。對此,可以作如下解釋:在不完全信息靜態博弈中,參與人同時行動,沒有機會觀察到別人的選擇。給定其他參與人的戰略選擇,每個參與人的最優戰略依賴於自己的類型。由於每個參與人僅知道其他參與人有關類型的分布機率,而不知道其真實類型,因而,他不可能知道其他參與人實際上會選擇什麼戰略。但是,他能夠正確地預測到其他參與人的選擇與其各自的有關類型之間的關係。因此,該參與人的決策目標就是:在給定自己的類型,以及給定其他參與人的類型與戰略選擇之間關係的條件下,使得自己的期望效用最大化。貝葉斯納什均衡是一種類型依賴型戰略組合。在給定自己的類型和其他參與人類型的分布機率的條件下,這種戰略組合使得每個參與人的期望效用達到了最大化。
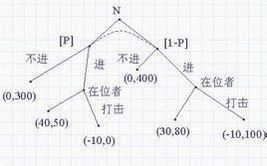
回到上面提到的市場進入的例子。在這個例子裡,對於挑戰者B來說,原壟斷者A在阻撓成本方面,存在著兩種可能性:高成本或低成本。B不知道A的阻撓成本究竟是高是低,但他知道A在這兩種不同阻撓成本下會作出的選擇,以及不同阻撓成本(類型)的分布機率。假定高成本的機率為x,則低成本的機率為(1-x)。如果A的阻撓成本高,A將默許B進入市場;如果A的阻撓成本低,A將阻撓B進入市場。在這兩種情況下,如表7-10所示,B進入的支付函式分別是得到40和失去10。因此,B選擇進入所得到的期望利潤為40x+(-10)(1-x),選擇不進入的期望利潤為0。簡單的計算表明,當A阻撓成本高的機率大於20%時,挑戰者B選擇進入得到的期望利潤大於選擇不進入的期望利潤。此時,選擇進入是B的最優選擇。此時的貝葉斯納什均衡為,挑戰者B選擇進入,高成本原壟斷者選擇默許,低成本原壟斷者選擇阻撓。
在動態博弈中,行動有先後次序,後行動者可以通過觀察先行動者的行為,來獲得有關先行動者的信息,從而證實或修正自己對先行動者的判斷。
如上所述,在不完全信息條件下,博弈的參與人知道其他參與人可能有哪幾種類型,也知道不同的類型與相應戰略選擇之間的關係。但他們並不知道其他參與人的真實類型。在不完全信息靜態博弈中,我們是通過海薩尼轉換,即通過假定其他參與人知道某一參與人的所屬類型的分布機率,來得出博弈的貝葉斯納什均衡結果的。而在不完全信息動態博弈中,問題變得更加簡單。博弈開始時,某一參與人既不知道其他參與人的真實類型,也不知道其他參與人所屬類型的分布機率。他只是對這一機率分布有自己的主觀判斷,即有自己的信念。博弈開始後,該參與人將根據他所觀察到的其他 。
方法
(1)一個虛擬的參與人“自然”,自然首先決定參與人的類型,賦予各參與人的類型向量 , 其中 t=(t1....tn),
(2)自然告知參與者i自己的類型,卻不告訴其他參與者的類型;
(3)參與者同時選擇行動,每一參與者i從可行集Ai中選擇行動方案 ;
(4)各方得到收益Ai(a1......ai,ti) 。
藉助於第一步和第二步中虛構的參與者“自然”的行動,我們可以把一個不完全信息的博弈表述為一個不完美信息的博弈。海薩尼轉換是處理不完全信息博弈的標準方法。
分析
海薩尼轉換是處理不完全信息博弈的標準方法。一般地,“自然”在博弈開始的時候選擇參與人的類型,參與人的某個類型包括表征類型的各個特徵如策略空間、信息集、得益函式等,這些又稱為該類型參與人所擁有的個人信息。
不完全信息意味著博弈各方中至少有一個參與人有多個類型。
通過海薩尼轉換,博弈開始時,所有參與人有關“自然”的行動有一致的信念,即都知道所有參與人類型的機率分布函式P(t1,t2,…,tn),此即“海薩尼公理”。
案例
舉例來說,某一市場原來被A企業所壟斷。B企業考慮是否進入。B企業知道,A企業是否允許它進入,取決於A企業阻撓B企業進入所花費的成本。如果阻撓的成本低,那么,正如下表後兩列所表示的,A企業的占優戰略是阻撓,博弈有重複剔除的占優戰略均衡——A阻撓,B不進入。如果阻撓的成本高,那么,正如表7-10前兩列所表示的,A企業的占優戰略是默許B進入,博弈有重複剔除的占優戰略均衡——A默許,B進入。B企業所不知道的,是A企業的阻撓成本是高是低。這裡,某一參與人本人知道、其他參與人則不知道的信息稱為私人信息。某一參與人所擁有的全部私人信息稱為他的類型。在上述例子中,阻撓成本就是 A的私人信息。高阻撓成本和低阻撓成本則是兩種不同的類型。
海薩尼轉換後的市場進入博弈
A高成本 低成本默許 阻撓 默許 阻撓
B 進入 40,50 -10,0 30,100 -10,140
不進入 0,300 0,300 0,400 0,400
顯然,在這裡,B所遇到的,是不確定性條件下的選擇問題。因為B不僅不知道A的類型(是高還是低),而且不知道不同類型的分布機率。