簡介
在計算機系統的發展過程中,曾經提出過多種方法表示實數,但是到為止使用最廣泛的是浮點表示法。相對於定點數而言,浮點數利用指數使小數點的位置可以根據需要而上下浮動,從而可以靈活地表達更大範圍的實數。 浮點數表示法利用科學計數法來表達實數 。
在IEEE-754標準出現之前,業界並沒有一個統一的浮點數標準,相反,很多計算機製造商都在設計自己的浮點數規則以及運算細節。
為了便於軟體的移植,浮點數的表示格式應該有一個統一的標準。1985年,IEEE(Institute of Electrical and Electronics Engineers,美國電氣和電子工程師協會)提出了IEEE-754標準,並以此作為浮點數表示格式的統一標準。幾乎所有的計算機都支持該標準,從而大大改善了科學應用程式的可移植性 。
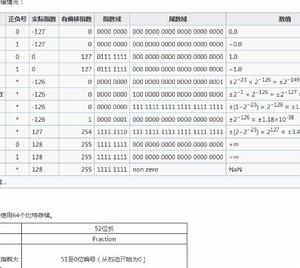
IEEE標準從邏輯上採用一個三元組{S, E, M}來表示一個數N,它規定基數為2,符號位S用0和1分別表示正和負,尾數M用原碼錶示,階碼E用移碼錶示。根據浮點數的規格化方法,尾數域的最高有效位總是1,由此,該標準約定這一位不予存儲,而是認為隱藏在小數點的左邊,因此,尾數域所表示的值是1.M(實際存儲的是M),這樣可使尾數的表示範圍比實際存儲多一位。為了表示指數的正負,階碼E通常採用移碼方式來表示,將數據的指數e 加上一個固定的偏移量後作為該數的階碼,這樣做既可避免出現正負指數,又可保持數據的原有大小順序,便於進行比較操作。
IEEE 754規定了四種表示浮點數值的方式:單精確度(32位)、雙精確度(64位)、延伸單精確度(43比特以上,很少使用)與延伸雙精確度(79比特以上,通常以80位實現)。只有32位模式有強制要求,其他都是選擇性的。大部分程式語言都有提供IEEE浮點數格式與算術,但有些將其列為非必需的。例如,IEEE 754問世之前就有的C語言,有包括IEEE算術,但不算作強制要求(C語言的float通常是指IEEE單精確度,而double是指雙精確度)。
該標準的全稱為IEEE二進制浮點數算術標準(ANSI/IEEE Std 754-1985),又稱IEC 60559:1989,微處理器系統的二進制浮點數算術(本來的編號是IEC 559:1989)。後來還有“與基數無關的浮點數”的“IEEE 854-1987標準”,有規定基數為2跟10的狀況。最新標準是“ISO/IEC/IEEE FDIS 60559:2010”。
標準
一個浮點數 (Value) 的表示其實可以這樣表示:
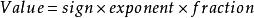 浮點數標準
浮點數標準也就是浮點數的實際值,等於符號位(sign bit)乘以指數偏移值(exponent bias)再乘以分數值(fraction)。
以下是IEEE 754對浮點數格式的描述。
比特的約定
 IEEE 754浮點數的三個域
IEEE 754浮點數的三個域把W個比特(bit)的數據,從記憶體地址低端到高端,以0到W−1編碼。通常將記憶體地址低端的比特寫在最右邊,稱作最低有效位(Least Significant Bit,LSB),代表最小的比特,改變時對整體數值影響最小的比特。聲明這一點的必要性在於X86體系架構是小端序的數據存儲。對於十進制整數N,必要時表示為N10以與二進制的數的表示N2相區分。
對於一個數,其二進制科學計數法表示下的指數的值,下文稱之為指數的實際值;而根據IEEE 754標準對指數部分的編碼的值,稱之為浮點數表示法指數域的編碼值。
整體呈現
二進制浮點數是以符號數值表示法的格式存儲——最高有效位被指定為符號位(sign bit);“指數部分”,即次高有效的e個比特,存儲指數部分;最後剩下的f個低有效位的比特,存儲“有效數”(significand)的小數部分(在非規約形式下整數部分默認為0,其他情況下一律默認為1)。
指數偏移值
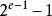 浮點數標準
浮點數標準 浮點數標準
浮點數標準指數偏移值(exponent bias),是指浮點數表示法中的指數域的編碼值為指數的實際值加上某個固定的值,IEEE 754標準規定該固定值為,其中的為存儲指數的比特的長度。
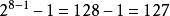 浮點數標準
浮點數標準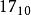 浮點數標準
浮點數標準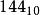 浮點數標準
浮點數標準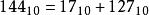 浮點數標準
浮點數標準以單精度浮點數為例,它的指數域是8個比特,固定偏移值是。此為有號數的表示方式,單精度浮點數的指數部分實際取值是從-127到128。例如指數實際值為,在單精度浮點數中的指數域編碼值為,即。
採用指數的實際值加上固定的偏移值的辦法表示浮點數的指數,好處是可以用長度為 {\displaystyle e} 個比特的無符號整數來表示所有的指數取值,這使得兩個浮點數的指數大小的比較更為容易,實際上可以按照字典序比較兩個浮點表示的大小。這種移碼錶示的指數部分,中文稱作階碼。
規約形式的浮點數
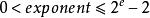 浮點數標準
浮點數標準 浮點數標準
浮點數標準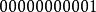 浮點數標準
浮點數標準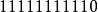 浮點數標準
浮點數標準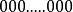 浮點數標準
浮點數標準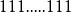 浮點數標準
浮點數標準如果浮點數中指數部分的編碼值在之間,且在科學表示法的表示方式下,分數 (fraction) 部分最高有效位(即整數字)是,那么這個浮點數將被稱為規約形式的浮點數。“規約”是指用確定的浮點形式去表示一個值。由於這種表示下的尾數有一位隱含的二進制有效數字,為了與二進制科學計數法的尾數(mantissa)相區別,IEEE754稱之為有效數(significant)。舉例來說,雙精度 (64-bit) 的規約形式浮點數在指數偏移值的值域為 (11-bit) 到,在分數部分則是到(52-bit)。
非規約形式的浮點數
如果浮點數的指數部分的編碼值是0,分數部分非零,那么這個浮點數將被稱為非規約形式的浮點數。一般是某個數字相當接近零時才會使用非規約型式來表示。 IEEE 754標準規定:非規約形式的浮點數的指數偏移值比規約形式的浮點數的指數偏移值小1。例如,最小的規約形式的單精度浮點數的指數部分編碼值為1,指數的實際值為-126;而非規約的單精度浮點數的指數域編碼值為0,對應的指數實際值也是-126而不是-127。實際上非規約形式的浮點數仍然是有效可以使用的,只是它們的絕對值已經小於所有的規約浮點數的絕對值;即所有的非規約浮點數比規約浮點數更接近0。規約浮點數的尾數大於等於1且小於2,而非規約浮點數的尾數小於1且大於0 。
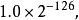 浮點數標準
浮點數標準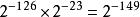 浮點數標準
浮點數標準 浮點數標準
浮點數標準 浮點數標準
浮點數標準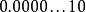 浮點數標準
浮點數標準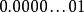 浮點數標準
浮點數標準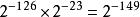 浮點數標準
浮點數標準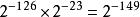 浮點數標準
浮點數標準除了規約浮點數,IEEE754-1985標準採用非規約浮點數,用來解決填補絕對值意義下最小規格數與零的距離。(舉例說,正數下,最大的非規格數等於最小的規格數。而一個浮點數編碼中,如果exponent=0,且尾數部分不為零,那么就按照非規約浮點數來解析)非規約浮點數源於70年代末IEEE浮點數標準化專業技術委員會醞釀浮點數二進制標準時,Intel公司對漸進式下溢出(gradual underflow)的力薦。當時十分流行的DEC VAX機的浮點數表示採用了突然式下溢出(abrupt underflow)。如果沒有漸進式下溢出,那么0與絕對值最小的浮點數之間的距離(gap)將大於相鄰的小浮點數之間的距離。例如單精度浮點數的絕對值最小的規約浮點數是它與絕對值次小的規約浮點數之間的距離為。如果不採用漸進式下溢出,那么絕對值最小的規約浮點數與0的距離是相鄰的小浮點數之間距離的倍!可以說是非常突然的下溢出到0。這種情況的一種糟糕後果是:兩個不等的小浮點數X與Y相減,結果將是0.訓練有素的數值分析人員可能會適應這種限制情況,但對於普通的程式設計師就很容易陷入錯誤了。採用了漸進式下溢出後將不會出現這種情況。例如對於單精度浮點數,指數部分實際最小值是(-126),對應的尾數部分從 {一直到、,相鄰兩小浮點數之間的距離(gap)都是;而與0最近的浮點數(即最小的非規約數)也是。這裡有三個特殊值需要指出:
如果指數是0並且尾數的小數部分是0,這個數±0(和符號位相關);
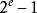 浮點數標準
浮點數標準如果指數 =並且尾數的小數部分是0,這個數是±∞(同樣和符號位相關);
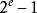 浮點數標準
浮點數標準如果指數 =並且尾數的小數部分非0,這個數表示為不是一個數(NaN)。
浮點數的比較
浮點數基本上可以按照符號位、指數域、尾數域的順序作字典比較。顯然,所有正數大於負數;正負號相同時,指數的二進制表示法更大的其浮點數值更大。
浮點數的捨入
任何有效數上的運算結果,通常都存放在較長的暫存器中,當結果被放回浮點格式時,必須將多出來的比特丟棄。 有多種方法可以用來運行捨入作業,實際上IEEE標準列出4種不同的方法:
捨入到最接近:捨入到最接近,在一樣接近的情況下偶數優先(Ties To Even,這是默認的捨入方式):會將結果捨入為最接近且可以表示的值,但是當存在兩個數一樣接近的時候,則取其中的偶數(在二進制中式以0結尾的)。
朝+∞方向捨入:會將結果朝正無限大的方向捨入。
朝-∞方向捨入:會將結果朝負無限大的方向捨入。
朝0方向捨入:會將結果朝0的方向捨入。
浮點數的運算與函式
下述函式必須提供:
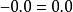 浮點數標準
浮點數標準加減乘除(Add、subtract、multiply、divide)。在加減運算中負零與零相等:
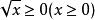 浮點數標準
浮點數標準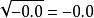 浮點數標準
浮點數標準 浮點數標準
浮點數標準平方根(Square root):,另規定浮點餘數。返回值。
近似到最近的整數 {\displaystyle round(x)}。如果恰好在兩個相鄰整數之間,則近似到偶數。
比較運算. -Inf <負的規約浮點數數<負的非規約浮點數< -0.0 = 0.0 <正的非規約浮點數<正的規約浮點數< Inf;
特殊比較: -Inf = -Inf, Inf = Inf, NaN與任何浮點數(包括自身)的比較結果都為假,即 (NaN ≠ x) = false.
建議的函式與謂詞
copysign(x, y): copysign(x, y)返回的值由x的不帶符號的部分和y的符號組成。因此abs(x)等於copysign(x, 1.0)。copysign可以對NaN正確操作,這是少有的幾個可以對NaN像普通算術一樣操作有效的函式之一。C99新增了copysign函式。
−x:從涵義上指將x的符號反轉。當x是±0或者NaN時,其涵義可能不同於0-x.
scalb(y, N):計算y×2N(N是整數),無需再計算2N。C99中對應的函式名是scalbn.
logb(x):計算x = 1.a×2n(x ≠ 0, a ∈[0, 1))中的n. C99新增了logb和ilogb函式。
nextafter(x,y):沿y方向找最鄰近x的可表達浮點數。比如nextafter(0, 1)得到的是最小可表達的正數。C99新增了nextafter函式。
finite(x):判斷x是否有限,即−Inf < x < Inf. C99新增了isfinite函式。
isnan(x):判斷x是否是一個NaN,這等價於"x ≠ x". C99新增了isnan函式。
x <> y:僅當x < y或者x > y時才為True,其涵義是NOT(x = y)。注意這不同於"x ≠ y"。
unordered(x, y):當x與y無法比較大小時為True,比如說x或者y是一個NaN. C99中對應的函式名是isunordered.
class(x):區分x的浮點數類屬:信號NaN、靜默NaN、-Inf、負的規約浮點數,負的非規約浮點數,-0.0,0.0,正的非規約浮點數,正的規約浮點數,Inf。