原理簡介
物理學的基本原理之一。介質中同時存在幾列波時，每列波能保持各自的傳播規律而不互相干擾。在波的重疊區域裡各點的振動的物理量等於各列波在該點引起的物理量的矢量和。
在兩列波重疊的區域裡，任何一個質點同時參與兩個振動，其振動位移等於這兩列波分別引起的位移的矢量和，當兩列波振動方向在同一直線上時，這兩個位移的矢量和在選定正方向後可簡化為代數和。
注意：只有當波的強度較小，波動方程變現為線性方程時，波的疊加原理才普遍成立。
疊加原理的方法
代數法
同頻率、同振動方向的單色光:
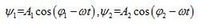波的疊加原理兩振動相加後，仍為簡諧振動。則有
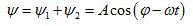波的疊加原理其中，
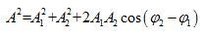波的疊加原理
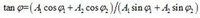波的疊加原理複數法
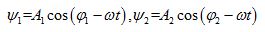波的疊加原理同樣可得1中的表達式。
振幅矢量法
在復空間中，求
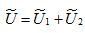波的疊加原理如下圖所示:
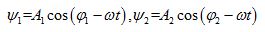波的疊加原理不同頻率單色波的疊加
振動方向相同、傳播方向相同，頻率不同的兩列波，
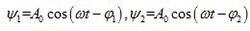波的疊加原理合成振動為：
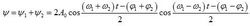波的疊加原理由於
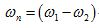波的疊加原理較小，它對
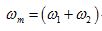波的疊加原理起調製作用，相當於頻率為ωm的波的振幅隨時間變化，如下圖示：
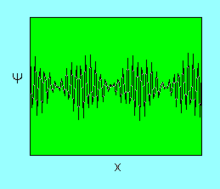波的疊加原理此時形成光學拍，拍頻為2ωm，強度分布隨時間和空間變化。
結論： 1、不同頻率單色光疊加形成光學拍；
2、不同頻率的定態光波疊加形成非定態光。
