波波夫超穩定性理論
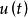波波夫超穩定性
波波夫超穩定性超穩定性理論討論的是系統輸入輸出乘積的積分值受限制的條件下的穩定性，1964年羅馬尼亞學者V.M.波波夫所提出。對於所研究的系統，如果用 表示輸入向量， 表示輸出向量，系統輸入輸出乘積積分值的限制關係可表示為：
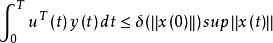波波夫超穩定性
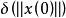波波夫超穩定性
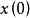波波夫超穩定性其中 表示依賴於初始狀態 的正常數。如果對於這種限制總能找到相應的正的常數 K和 δ,使狀態向量滿足：
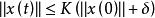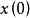波波夫超穩定性 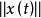波波夫超穩定性
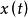波波夫超穩定性
波波夫超穩定性
波波夫超穩定性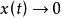
波波夫超穩定性這種系統便被稱為超穩定的。其中 是系統的初始狀態， 是狀態向量 的範數。如果 時,還有 ，則稱系統是超漸近穩定的。超穩定性理論適用於一切類型的控制系統，包括線性系統和非線性系統、定常系統和時變系統。超穩定理論的一個重要套用領域是模型參考適應控制系統。
正實性
相關對於線性定常系統，系統的超穩定性與其傳遞函式矩陣的正實性之間有著密切關係。澳大利亞學者B.D.O.安德森在1968年證明，在滿足輸入輸出乘積積分值的限定情況下，系統的超穩定性等價於系統傳遞函式矩陣的正實性，系統的超漸近穩定性等價於系統傳遞函式矩陣的嚴格正實性。
正實性和嚴格正實性是現代網路理論中的兩個重要概念。一個傳遞函式矩陣 G (s)為 正實矩陣的條件是：對於滿足 Re s>0 的複數 s都成立
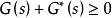波波夫超穩定性
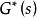波波夫超穩定性
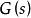波波夫超穩定性其中 是 的共軛轉置矩陣。如果存在λ>0，使得所有的Re s>-λ，都成立上式，則 G (s)為 嚴格正實矩陣。
也就是說，對於某一有理分式矩陣G(s)，如果是正實函式矩陣，則要求
1）在右半開平面，G(s)的每個元素都是解析的，即每個元素在右半平面都沒有極點；
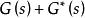波波夫超穩定性2）對於右半平面上所有的s，是半正定的Hermite矩陣。
嚴格正實函式的定義類似，不同之處在於要求右半閉平面。
