波束形成算法的分類
波束形成算法是智慧型天線研究中最核心的內容。按照不同的準則，可以將波束形成算法分為許多種類。例如根據基於的對象不同，可將波束形成算法分為以下3類 。
（1）基於方向估計的自適應算法。這類算法分為兩種情況。第一種情況，參考用戶信號方向已知。這時可根據不同的準則（如線性約束最小方差準則、最大似然準則和最大信噪比準則等）計算自適應權值。第二種情況，參考用戶信號方向未知。這時可根據多信號分類（MUSIC）、旋轉不變技術信號參數估計（ESPRIT）等方法等估計信號DOA。這類方法雖然在分析上較方便，但是存在運算複雜度高、對誤差敏感度高等問題。
（2）基於訓練信號或者參考信號的方法。這類算法不需要估計信號到達方向，對天線本身的結構也沒有太多的限制。但是這類算法存在的問題是發射訓練信號需要先驗載波和符號的恢復，這對於存在同信道干擾的情況比較困難，而且發射訓練信號會降低頻譜的利用率。
（3）基於信號結構的波束形成方法。這類算法利用信號的時域特性來計算權值，利用了恆模特性、有線集碼、循環平穩特性和高階統計量等，對誤差比較穩健，不需要信號的方向信息。但是，這類算法存在的問題是收斂速度較慢。
另一種更常用的分類方法是根據是否需要發射參考信號，將波束形成的算法分為非盲算法和盲算法。
（1）非盲算法通過發射訓練序列或者導頻信號來確定信道回響，然後根據一定的準則調整權值。常用非盲算法包括最小均方（LMS）算法、直接矩陣求逆（DMI）算法和遞歸最小二乘（RLS）算法。
（2）盲算法不需要發射訓練序列或者導頻信號，接收端將自己傳送的信號作為參考信號進行估計，然後調整權值。典型的盲算法包括兩種：一種是利用信號特徵的盲算法，比如利用信號恆模特性的恆模算法，利用信號循環平穩性的周期平穩性算法，還有有限符號集算法；另一種是利用DOA的盲算法。提取DOA信息的算法如MUSIC、ESPRIT等。
波束形成算法的分類如圖1所示。
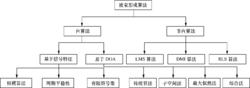波束形成算法圖1波束形成算法分類
以下分別介紹幾種典型的波束形成算法。值得首先一提的是，由於在實際通信系統中，信號的幅度、相位和到達角等都以極快的速度變化，這要求自適應網路的回響速度要極快。所以，對於一種確定的算法，其收斂速度是衡量其好壞的一個重要標準。另一重要標準是穩態回響。自適應陣的穩態回響可以通過方向圖、均方誤差、輸出SINR等來衡量。
非盲算法
（1）LMS算法
LMS算法基於最小均方誤差（MMSE）準則，根據最陡下降法原理得出。下一時刻的加權矢量等於當前時刻的加權矢量加上一個負均方誤差梯度的比例項，如式（2.8）所示 ：
W（n+1）=W（n）-μ▽（n） （2.8）
式中，▽（n）表示代價函式的梯度。代價函式是指在一個最最佳化波束形成器中，通過使用代價函式（如均方誤差）最小化來實現方向圖的形成。通常，這個代價函式反比於陣列的輸出。這樣，當代價函式最小時，陣列輸出端的信號質量就達到最優。梯度的計算是複雜的，通常用適當的估計值▽（n）來代替，若取
▽（n）=-2e（n）X（n） （2.9）
式中，e(n)為期望輸出d(n)與濾波器實際輸出之間的誤差，X(n)為輸出信號，則式（2.8）變為：
W(n+1)=W（n）+2μe（n）X（n） （2.10）
選擇合適的步長μ，就可以由一個初始加權矢量W(0)經過若干次疊代後，得到一定精度要求下的最佳加權矢量。
LMS算法是數位訊號處理中最經典的算法之一，其主要優點是能穩定收斂，比較靈活，易於實現。但是，存在對輸入信號協方差矩陣特徵值分布敏感，收斂速度較慢的問題。
（2）DMI算法
LMS算法通過疊代來實現波束形成，對於系統實時性的要求有時難以得到滿足，而DMI算法對協方差矩陣直接求逆，可加速收斂速率。
如果期望信號和干擾信號都先驗已知，即可求得其協方差矩陣。但是在實際系統中，信號未知且信道時變，自適應處理必須不斷更新加權矢量來適應動態的環境。這需要在沒有先驗知識的情況下，以及在有限的觀察時間內，得到自相關和互相關的估計，並利用估計值得到加權矢量。具體算法如下所示 ：
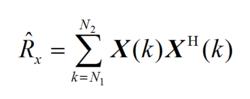波束形成算法（2.11）
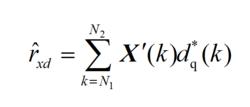波束形成算法（2.12）
式中，R是X(K)自相關矩陣的估計，r是向量X(k)和期望信號估計dq(k)的互相關向量的估計。N1和N2為觀察時間的下限和上限。其最優加權矢量如式（2.13）所示：
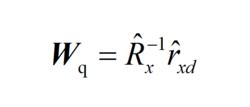波束形成算法（2.13）
DMI算法比LMS算法的收斂速度快得多，但是由於需要矩陣求逆運算，存在複雜度高的問題。
（3）RLS算法
DMI算法中，自相關和互相關矩陣的估計使用的是觀察窗，在觀察窗內認為每次採樣的數據對估計有相同的貢獻。但在時變信道中，這樣處理可能會造成數據的損失。
在RLS算法中，通過數據加權的方式獲得估計，新信息有較大的權值；並且用一個與信號相關的附加矩陣代替LMS算法中的步長，提高了收斂速率。RLS算法的加權矢量疊代式為 ：
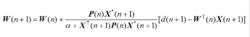波束形成算法（2.14）
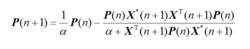波束形成算法（2.15）
式中，d(n)代表參考信號，P(n)為疊代過程中的過渡矩陣，其中α稱為遺忘因子（α≤10）。
RLS算法的優點是收斂速度快，但是存在計算量大、不能穩定收斂等問題。
盲算法
（1）基於信號特徵的盲算法
利用信號的一些固有特徵，如恆模特性、周期平穩性、高斯性、有限字元和獨立性等，在接收端通過這些特徵的恢復而抑制干擾的算法就是基於信號特徵的盲算法。這類基於信號特徵的盲算法可以分為兩種：一種是利用信號的統計性質（如非高斯性和循環平穩性），稱為隨機性盲波束形成；第二種是利用信號本聲的確定性性質（如恆模、有限字元、獨立性等）或信道的信號處理模型的結構性質，稱為確定性盲波束形成。
以下主要介紹一種套用廣泛的最小二乘恆模算法。
一般的恆模算法（CMA）是基於MMSE準則的，一種基於最小二乘（LS）準則的最小二乘恆模（LSCMA）算法得到了更廣泛的套用。
LSCMA的代價函式可以表示為 ：
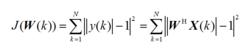波束形成算法（2.16）
式中，N代表快拍個數。
這裡可以分為靜態LSCMA和動態LSCMA兩種情況。靜態LSCMA在疊代過程中輸入信號存儲器中的值保持一個固定序列；動態LSCMA在一次疊代過程中輸入信號存儲器中的值在不斷更新。具體表達式如下所示 ：
靜態LSCMA：
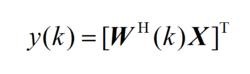波束形成算法（2.17）
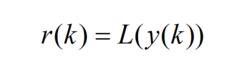波束形成算法（2.18）
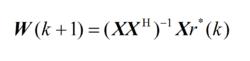波束形成算法（2.19）
動態LSCMA：
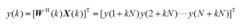波束形成算法（2.20）
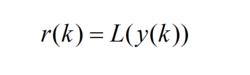波束形成算法（2.21）
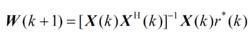波束形成算法（2.22）
其中，
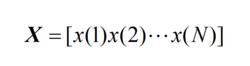波束形成算法（2.23）
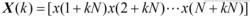波束形成算法（2.24）
分別代表靜態和動態情況下的輸入信號矢量。
r(k)代表對輸出信號進行歸一化處理，如下式所示：
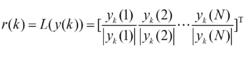波束形成算法（2.25）
比較以上公式可以看出，靜態LSCMA算法較動態LSCMA簡單，但是信道隨著時間變化較快時，使用靜態LSCMA會丟失很多有用信息，很可能形成不正確的波束。所以，動態LSCMA在實際系統中得到更多套用。
當然，也可用輸入信號的自相關矩陣和輸入、輸出信號之間的互相關矩陣來表示加權矢量更新公式，如下式所示：
波束形成算法（2.26）
其中，
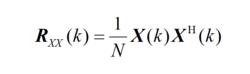波束形成算法（2.27）
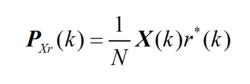波束形成算法（2.28）
通過以上分析可以看出，由於LSCMA算法使用了DMI的方法，避免了LMS算法對輸入信號協方差矩陣特徵值分布敏感的問題，收斂速度較快，而且不同於基於MMSE準則的一般CMA算法，LSCMA算法能夠穩定收斂。
（2）基於DOA的盲算法
基於DOA估計的自適應波束形成算法，首先根據陣列信號的先驗知識估計信號的DOA，然後根據這些估計信息建立最優波束器從干擾和噪聲中分離出期望信號。用於DOA估計的高解析度技術有傳統法（比如延遲相加法和Capon最小方差法）、子空間法（比如MUSIC算法和ESPRIT算法）、最大似然法以及將特性恢復法和子空間結合起來的綜合法。傳統法基於經典波束形成算法，需要大量的陣元才能獲得高分辨。子空間利用輸入數據矩陣的特徵結構，是高解析度的次最優方法。最大似然是最優方法，即使在信噪比很低的環境下也能獲得良好的性能，但是存在計算量大的問題。綜合法首先利用特徵恢複方案區分多個信號，估計空間特徵，進而採用子空間法確定波達方向。總體而言，基於DOA估計的自適應波束形成算法分為兩步：DOA估計和波束形成，計算量較大。此外，很難準確獲得這類算法需要的先驗空間特性知識 。
以下主要介紹傳統的Capon算法和套用較為廣泛的MUSIC算法。
①Capon算法。Capon波束形成器（即最小方差無畸變回響波束形成器）使用部分自由度在期望的觀測方向上形成一個波束，利用剩餘的自由度在干擾方向上形成零陷。當有多個信號入射感測器陣列時，陣列輸出功率將包括期望信號功率和干擾信號的功率。Capon最小方差法使干擾信號的輸出功率最小，以抑制干擾信號，同時使增益在觀測方向保持為常數（通常設這個常數為1），用下式表示 ：
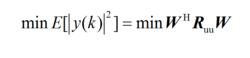波束形成算法（2.29）
約束條件：
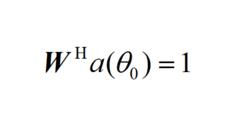波束形成算法（2.30）
式（2.29）是一個約束最佳化問題轉化為非約束問題，利用拉格朗日乘子，可以得到：
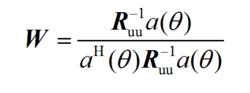波束形成算法（2.31）
利用Capon波束形成方法，陣列輸出功率關於DOA的函式可由Capon空間譜得到：
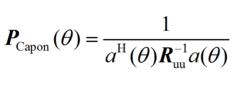波束形成算法（2.32）
把所有值取遍，計算和畫出Capon譜，就可以通過尋找譜上的峰值來估計出DOA。
Capon算法雖然經典，但是存在一些不足，比如不能很好地區分期望信號和與期望信號相關的其他信號，因為它在減小處理器輸出功率時無意中利用了這種相關性，而沒有為其形成零陷。即在使輸出功率達到最大的過程中，相關分量可能會惡化合併。而且，Capon法需要對矩陣求逆運算，這對於大型矩陣計算相當複雜 。
②MUSIC算法。MUSIC算法是一種有代表性的空間譜算法，是空間譜估計發展史上具有重要意義的算法，實際上已經成為空間譜估計方法和理論的重要基石。其算法流程如下 ：
（a）根據N次快拍的陣列輸入數據X(n)，n=0,1,…,N−1，計算輸入協方差矩陣的估計值 ：
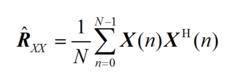波束形成算法（2.33）
（b）對進行特徵分解：
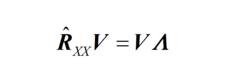波束形成算法（2.34）
其中，
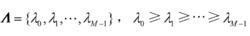波束形成算法為R的特徵值，V=[qqq]是相應的特徵向量。
（c）利用最小特徵值λmin的重數N得到信號數的估計值K=M-N。
（d）計算MUSIC譜：
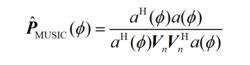波束形成算法（2.35）
其中，Vn=[qq...,q]。
（e）搜尋P(Φ)的K個最大峰值，得到波達方向的估計，k=0,1,…,−1。
MUSIC算法利用了信號子空間的特徵空間，性能優越。但是，當入射信號高度相關時，由於R變成奇異，MUSIC算法也將失效。總體而言，MUSIC算法具有解析度高的優點，但是也存在一些不足，比如抗多徑能力弱，無法分辨相關信號源，當信號源數大於陣元數時，算法失效等。
