泛概括定理(pan-comprehension theorem ) 中介公理集合論的一條基本定理.泛概括定理是泛概括公理的特殊情況:對任何NorP(二，t)，只要其中不包含a的自由出現，則
泛概括定理直觀地說，泛概括定理指任何正規謂詞均有一概集.此外，在MS系統中，由泛概括定理可進一步證明下述定理:對任何NorP(x,t)，只要其中不包含 a的自由出現，則
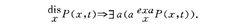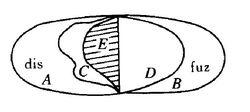
泛概括定理泛概括定理表明，在MS系統中，任何正規清晰謂詞，必有一集A，使得A是該謂詞的恰集.另一方面，在MS系統中，又能嚴格證明，任何康托爾意義下能用來造集的謂詞都是MS系統意義下的正規清晰謂詞.亦即MS系統中的正規清晰謂詞囊括了一切康托爾意義下的造集謂詞，而且正規清晰謂詞的外延大於康托爾意義下之造集謂詞的外延.由於 MS系統中有定理} disP V fuze，故所有謂詞分為清晰謂詞(A)和模糊謂詞(B)兩類。在正規限制下(如圖)，
泛概括定理有正規清晰謂詞 (C)及正規模糊謂詞(D)兩類.而圖中陰影部分(E)表示康托爾意義下的一切造集謂詞，C包括了E.因此，再看上述定理的結論(在MS系統中，任何正規清晰謂詞必有惟一確定的恰集)可知，MS系統中的泛概括公理又在實際上全面保留了康托爾意義下概括原則的內容.這樣，“在MS系統中是否會出現悖論”的問題就可做出肯定的回答:不會.在MS系統中已嚴格證明，歷史上任何邏輯數學悖論，以及在二值系統內無需解釋的多值邏輯悖論和無窮值悖論，均可在MS系統中排除(參見“悖論”).從而，人們一直在尋找一種如何修改概括原則的方案，使之既能排除古典集合論中的悖論，又能最大限度地保留概括原則的合理內容，這一問題終於在MS系統中得到了解決(參見 “中介公理集合論”).
