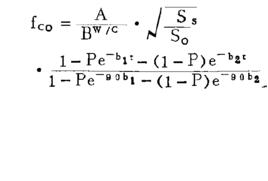簡介
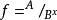 水灰比定律
水灰比定律水灰比定律是1 9 1 8 年美國波特蘭水泥協會( PCA ) 創建初期的混凝土專家阿伯拉姆氏提出的。這個定律影響深遠, 幾乎每一個混凝土工作者都能背誦: “ 在一定的材料和試驗條件下, 只要混凝土混合物是塑性的, 混凝土的強度則取決於拌和水的數量” , 其公式為: ,式中,f為6英寸直徑、12 英寸高(15*30厘米)圓柱體試件的抗壓強度, A 和B ——常數, 隨水泥質量、齡期、養護、試驗等方法不同而不同, X ——水灰比( w / c ) , 按體積計。
1 9 3 4年波特蘭水泥協會重申水灰比定律應是: “ 在一定的工作條件下, 集料品質和配合比不變時, 塑性混凝土的強度與其它性質, 都可由水灰比決定” 。而後又將水灰比值從體積比改為重量比。
直到上世紀八十年代, 這個定律一直在世界各國的混凝土界沿用著, 但是也一直被許多混凝土學者議論著。最近在有些國家似乎又出現議論的熱潮。我們對於這些議論, 也不能當作街談巷議而等閒視之, 若是認真分析一下, 也許能從中尋覓到一些有用的材料。
水灰比定律的實效
嚴格地說, 阿伯拉姆氏的水灰比定提出時, 已有足夠多的實驗數據, 並製成系統的曲線, 導出可以定量的公式, 但與其它自然科學一般的定律比較, 容易發現它的破綻, 似乎還不足以達到稱之為定律的程度。比如, 當時阿伯拉姆氏認為混凝土強度與集料的粒徑和用量都無關係, 只有當集料的性質影響到混凝土的需水量時, 才能間接地影響混凝土的強度; 後來有人就從這一點出發, 指出在水灰比定律中過於簡化了影響混凝土強度的各項因素的關係, 特別是忽視了集料的作用。
其實, 對水灰比定律提出的種種指責, 都還沒有從根本上撼動這個定律在實用中的地位。但看水灰比定律的形成過程: 阿伯拉姆氏是為混凝土配合設計的要而提出來的, 有人評論當時阿伯拉姆氏對混凝土技術一舉作出三大貢獻, 一是水灰比定律, 二是細度模數配合設計法, 三是坍落度試驗法; 但是比較成功的只有兩個半。其中水灰比定律和坍落度試驗兩者一直被沿用, 當然是屬於成功的, 但是細度模數配合設計法卻嫌不夠簡捷, 而用細度模數估計細集料的粗細程度, 大家還認為有一定的實用價值, 只能算半個。因此說多少年來實踐考驗證實, 用水灰比定律的公式, 估算混凝土強度, 用水灰比最大限值, 保證混凝土耐久性, 確是簡單而有實際效益的。再從近代理論上說, 水泥漿體的強度取決於水灰比和水泥的水化程度, 但水化程度相同的水泥漿體, 其強度就主要取決於水灰比。至於混凝土的強度, 固然是取決於水泥漿體的強度, 還有漿體和集料界面的結合強度, 也還有集料的影響。漿體強度既取決於水灰比, 同時水灰比也對界面強度起決定性的作用, 因此說, 若不考慮集料的影響, 那么混凝土的強度還是主要取決於水灰比。再說一般集料的強度總是遠遠超過水泥漿體的強度, 於是在普通混凝土中集料對混凝土強度影響的程度是有限的, 所以對於集料最大粒徑在一定範圍內(10~ 30 毫米) 的普通混凝土的強度而言, 水灰比仍是主要的影響因素。當然, 採用粒徑較大的粗集料或者套用輕集料時, 水灰比與強度的關係式中, 常數A和B , 就要加以修正了。這樣, 從實效來看, 可以認為阿伯拉姆氏獨具慧眼, 是首先識別水灰比實用價值的重要歷史人。
水灰比定律發展史
現階段的水灰比與強度的關係式也並非完全來自阿伯拉姆氏的水灰比定律, 試舉下列一些我們比較知名的混凝土學者所提出的水灰比關係式便可說明。
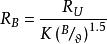 水灰比定律
水灰比定律( l ) 別遼也夫公式蘇聯別遼也夫在3 0年發表的雙曲線型水灰比公式, 基本與阿伯拉姆氏公式相同:
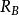 水灰比定律
水灰比定律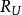 水灰比定律
水灰比定律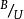 水灰比定律
水灰比定律式中, — 混凝土的抗壓強度, ——水泥的標號, ——水灰比(重量比),K——常數,用碎石時是3.5,用礫石時為4.0。此式將水泥標號這個因素, 從常數中分列出來, 而常數值成為粗集料因素, 由於計算時仍嫌麻煩, 實際上是利用繪製的關係曲線或查表方法。
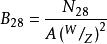 水灰比定律
水灰比定律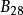 水灰比定律
水灰比定律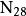 水灰比定律
水灰比定律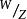 水灰比定律
水灰比定律( 2 ) 格拉夫公式德國的格拉夫在1 9 3 0年前後, 建議採用以下公式: ,式中, ——混凝土28 天抗壓強度, ——水泥標號, ——水灰比(重量比),A——常數,4-8.此式與別遼也夫公式的區別, 僅在於德國採用的水泥試驗方法與當時蘇聯硬練砂漿試驗不同。
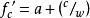 水灰比定律
水灰比定律( 3) 雷芝公式當保羅米公式在歐洲傳播之際, 無獨有偶的事情發生了, 即著名的挪威混凝土學者雷芝將阿伯拉姆氏公式演變為與保羅米公式幾乎雷同的直線關係式, 在美國廣為流傳, 稱為雷芝灰水比公式: .
保羅米公式或雷芝公式異途同歸, 便於實用, 從此許多國家各自發展了適合國情的灰水比公式, 列人規程; 或者有些大型工程或混凝土工廠, 根據試驗結果, 過數理統計處理, 自列“ 經驗公式” , 只不過常數不同而已.
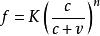 水灰比定律
水灰比定律( 4 ) “ 水泥空間比” 學說美國泰爾博特等最初也是根據菲萊” 特水泥空隙比理論, 發表了“ 水泥空間比公式: .上式中所謂水泥空間比, 實際上是單位體積的新拌混凝土中水泥的絕對體積與水泥漿的絕對體積之比, K = 2250公斤/平方厘米“ , n = 2.5。泰爾博特強調了混凝土結構中空隙的重要影響, 又提出了“ 基準水量” 和“ 相對水量” 等觀點和實驗數據, 更進一步接近現代混凝土強度理論,可是儘管當時在理論上領先, 而他們所建議的方法套用時必需建立四個關係曲線,相當費事, 終於不能普遍推廣。菲萊特和阿伯拉姆氏兩說, 最初看來“ 各有於秋” , 最後終於“ 合二為一” ,我們還應歸功於眾多的孜孜不倦的混凝土技術領域的耕耘者, 同時也不應忘記混凝土技術歷史上的那段從啟蒙到發展的鼎盛春秋。
近代發展情況
1 . “ 膠空比” 學說
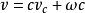 水灰比定律
水灰比定律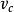 水灰比定律
水灰比定律 水灰比定律
水灰比定律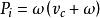 水灰比定律
水灰比定律恰恰是在當年阿伯拉姆氏所在的那個美國波特蘭水泥協會中, 以後有個成為該會主要學者的鮑威斯, 並不追隨阿伯拉姆氏的水灰比定律, 卻發展了與菲萊特的水泥空隙比學說一脈相承的“ 膠空比” 學說, 並考慮到了水泥水化程度( 參閱現代混凝土技術特寫之二“ 水泥漿體和微混凝土”)試將膠空比公式進一步分析, 不難發現, 新拌水泥漿體的初始空隙率仍然是主要取決於水灰比, 即漿體中的相對水量。新拌水泥漿體的體積, 等於水泥和拌和水體積之和, 算式如下 :式中,c——水泥的用量; ——水泥的比容( 比重的倒數) , ——水灰比。而初始空隙( Pi ) 的算式是: 當然, 水泥漿體的空隙與水化程度有關, 但在同一水化程度條件下, 水泥漿體的空隙率取決於初始空隙, 也即取決於水灰比。這樣表明水泥漿體強度與水灰比的關係, 完全類似強度與空隙率的關係。根據這樣的關係所繪成的水泥漿體強度S( 以對數表示) 與相應水灰比的直線關係圖, 即10 9 5 = A 一B (W / C ) , 它與阿伯拉姆氏的水灰比公式關係圖, 幾乎一模一樣, 也說明了膠空比學說與水灰比定律密切的血緣關係。
2.引氣穿昆凝土的水灰比
有人提出, 水泥空隙比學說較適用於引氣混凝土, 而近年研究結果, 表明水灰比定律的公式略加補充, 也可妥善解決這個問題。即引氣混凝土的水灰比可寫成( W 十△A )/ C。一般情況下, 即使是搗實程度較好的普通混凝土, 也會含有一部分空氣量, 通常由於集料的最大粒徑的不同, 這部份空氣量為10 ~ 30 升/ 立米, 混凝土中最佳含氣量變化範圍為45 ~ 65 升/立米, 因此通常△A = 35 升/ 立米。
3 . 模式的突破
許多人指出水灰比定律在實用中最大的缺點就是在理論上水灰比定律是以均勻的混凝土結構為前提, 而實際上由於泌水和粗集料的沉降作用在往會引起不均勻現象。為此學者們強調引氣劑的作用,呼籲大家注意當前只重推廣減水劑而忽視引氣劑的狀況。此外, 日本混凝土工程界正在積極發展“ 灰漿裹砂混凝土” (S E C混凝土) , 其原理是使用專門的砂料控制器, 將砂的含水量控制在恆定的範圍內,再將帶有適量表面水份的砂子, 與水泥、粗集料共同攪拌, 於是水泥就粘著在砂粒的表面上, 形成一層水灰比較小的水泥漿表殼, 然後再加入其餘的拌和水量以及必需的外加劑, 最後攪拌成灰漿裹砂混凝土。在這種混凝土中水灰比較小的水泥漿殼砂粒互相粘連起來, 可以把水灰比和流動性較大的稀漿體, 封閉在砂粒間的空隙中。裹砂的灰漿水灰比在0.15 至0.25 之間, 如用流變學原理解釋, 水灰比過低不能包滿砂粒, 水灰比過高則發生流淌。試驗結果表明, 不僅由於砂粒間粘結強度提高而使混凝土強度提高, 而且會在流動性較大的情況下, 幾乎一點也不發生泌水和集料沉降現象。它還適用於噴射混凝土。有人認為此法對水灰比定律有所突破, 但考其實質, 關鍵在於降低了砂粒表層灰漿水灰比, 也即提高了漿體和砂粒的界面結合強度, 這方面仍是受到水灰比定律支配的。但是對原來的水泥漿體均勻分布的式有所突破。