水文估計量的抽樣誤差
正文
水文隨機變數的分布函式中的參數(或參數的函式)的估計量的均方根誤差。水文隨機變數x的分布函式F(x，θ) 中所含的參數θ，一般皆為未知數, 需根據樣本資料(x1，x2，…，xn)予以估計。換言之,為進行參數估計，必須構造一個樣本的函式，稱為估計量，記為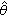
(x1，x2，…,xn)，從而當有一具體樣本(x1，x2,…,xn)之後,就可算出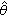(x1，x2，…，xn),做為θ的估計值。由於樣本為隨機變數，可以證明,作為樣本函式的估計量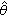(x1,x2，…，xn)，也是隨機變數，故有其機率密度函式，記為g(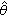，θ)，稱為抽樣分布（見上頁圖）。它表示估計量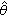取各種不同數值的可能性大小。雖然任一估計量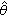取得真值θ的機率都為零, 但不同的估計量其平均誤差的大小還是不同的。這個平均誤差,通常以估計量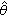對參數真值θ的均方根誤差來代表，可表示為：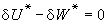 
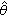，θ)的圖形對θ越集中, σ孌越小,反之則越大。 
水文估計量的抽樣誤差後, 就可進一步求得xp的估計量憫p。類似於對σ孌的討論,通常以估計量憫p對真值xp的均方根誤差來代表憫p的平均誤差，記為σ憫p。σ孌特別是σ憫p的數值，在分布函式及估計方法都很簡單時,可用分析方法採用近似公式予以計算。在分布函式或估計方法較複雜時，用近似公式計算，誤差較大。這時可用蒙特卡洛方法求出其近似值。水文統計學研究的基本內容之一，就是要設法提出一種抽樣誤差最小的估計量。