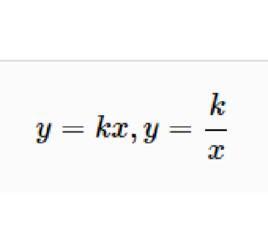正比例中的比例係數
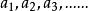 比例係數
比例係數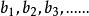 比例係數
比例係數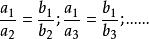 比例係數
比例係數正比例:兩種相關聯的量,當一種量的任意兩個數值的比,等於另一種量對應的兩個數值的比,那么這樣的兩種量就叫做 成正比例的量。用表示量A的值,表示量B的對應值,如果那么A、B兩種量就是 成正比例的量。
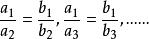 比例係數
比例係數因為
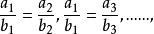 比例係數
比例係數顯然
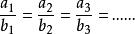 比例係數
比例係數所以。
由此可以看出,這些比的比值相等。
用y和x表示兩種相互關聯的量,如果這兩種量中相對應的兩個數的比值一定,那么y和x就成正比例。用k表示比值,這個關係可以表示成:
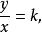 比例係數
比例係數或者
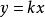 比例係數
比例係數 比例係數
比例係數常數叫做 比例係數。
反比例中的比例係數
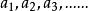 比例係數
比例係數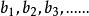 比例係數
比例係數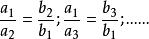 比例係數
比例係數兩種相關聯的量,當一種量的任意兩個數值的比,等於另一種量對應的兩個數值的反比,那么這樣的兩種量就叫做 成 反 比例的量,用表示量A的值.表示量B的對應值,如果那么A、B兩種量就是 成反比例的量。
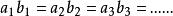 比例係數
比例係數由此可看出,。
 比例係數
比例係數用y和x表示兩種量,如果這兩種量中相對應的兩個數值的積一定,那么y和x就成反比例,用表示這個積,這個關係可以表示為:
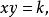 比例係數
比例係數或者
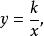 比例係數
比例係數 比例係數
比例係數常數也叫做 比例係數。
關於物理單位的比例係數
在物理學的方程式中都包含有 比例係數,所包含的比例係數與單位的選擇有關。在定義方程式中,包含的比例係數是一個永遠無量綱的量,它的數值是表示被量度的量的一種單位比另一種單位大到多少倍。例如,若方程中所有各量均用一種制的單位來表示,則此例係數等於1,若各量是用不同單位制表示,則係數不等於1。速度公式
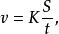 比例係數
比例係數所以
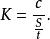 比例係數
比例係數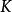 比例係數
比例係數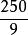 比例係數
比例係數當S用厘米、t用秒、v用千米/小時表示,則=(千米/小時)/(厘米/秒)=。
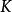 比例係數
比例係數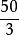 比例係數
比例係數當S用米、t用秒、v用千米/分表示,則=(千米/分)/(厘米/秒)=。
所以為了避免因係數而招致的麻煩,所有包含在一個公式中的量,在計算時要用同一種單位制來表示,計算結果也將是同一單位制,此例係數(K=1)可以略去不寫。
大多數物理學方程式,屬於定義方程式之列,在少數本來也可以成為定義方程式而不屬於定義方程式的物理學公式中,其比例係數是用實驗方法測定的,它是一個不等於1、有量綱、而且是具有一定物理意義的常數。例如萬有引力定律
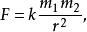 比例係數
比例係數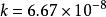 比例係數
比例係數由子力的單位已經由牛頓第二定律作了規定,於是萬有引力定律雖然也是表示力,就不能成為力的單位的定義方程式。因此公式中的此例係數k就不能等於1,而且還有量綱。1798年開文迪許第一次測定了它的數值,稱為 引力常數:厘米 克 秒 它表示質量各為1克、相距1厘米的兩質點,相互作用力的大小值。
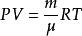 比例係數
比例係數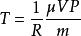 比例係數
比例係數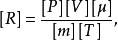 比例係數
比例係數還有克拉珀龍定律公式,可寫成。由於在歷史上溫度的單位是獨立選定的,所以不能令R等於1。這一個被稱為普適氣體常數的係數,也是用實驗的方法測定的。其量綱式它表明一克分子理想氣體,當溫度升高1℃時,在等壓膨脹的情況下所作的功的大小。