基本概念
歸謬式推理(inference with absurdity)是這樣一種推理,它的前提是兩個充分條件假言判斷,其前件相同,後件相矛盾,而結論是與這兩個假言判斷的前件相矛盾的判斷。例如:
如果大前提特稱,小前提否定能得出結論,那么大前提中的大項應該周延;
如果大前提特稱,小前提否定能得出結論,那么大前提中的大項不能周延;
所以,大前提特稱,小前提否定不能得出結論 。
歸謬式推理的邏輯形式
歸謬式推理的邏輯形式表示如下 :
如果p,那么q
如果p,那么非q
所以,非p
或用公式表示為:
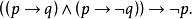 歸謬式推理
歸謬式推理或者
如果非p,那么q
如果非p,那么非q
所以,p。
歸謬式推理的套用與舉例
歸謬式推理形式在論證中經常使用,當我們反駁某一判斷時,可以先假設這個判斷是真的,並從這種假設中同時引伸出兩個相矛盾的判斷,再從這兩個判斷的矛盾性推出被反駁的判斷必然是假的。比如,有人認為“一切判斷都是假的”。我們就可以用歸謬式推理來駁斥他,先假設這個判斷是真的,即如果“一切判斷是假的”這一判斷是真的,那么“一切判斷都是假的”;如果“一切判斷都是假的”這一判斷是真的,那么“並非一切判斷都是假的”(有的判斷不是假的),所以,“一切判斷都是假的”不是真的
【例1】如果張三作案,那么李四一定是主犯;如果張三沒作案,那么王五參與作案。如果李四不是主犯,那么王五沒有參與作案 。
由此可推出以下哪項?
A.張三沒作案
B.李四一定是主犯
C.李四不一定是主犯
D.王五參與作案
E.張三作案
解析:
首先把題乾中第一句話“如果張三作案,那么李四一定是主犯”變為:“如果李四不是主犯,那么張三沒作案”;再與題乾中的第二句話“如果張三沒作案,那么王五參與作案”進行推理得:“如果李四不是主犯,那么王五參與作案”;這樣與第三句話:“如果李四不是主犯,那么王五沒有參與作案”構成歸謬式推理,即:
如果李四不是主犯,那么王五參與作案,
如果李四不是主犯,那么王五沒有參與作案,
所以,李四是主犯 。
【例2】義大利物理學家伽利略推翻古代“物體下落速度與重量成正比”(p)這一錯誤理論時運用的就是歸謬式推理。伽利略設計了一個實驗:A、B兩塊石頭,並且A重於B,把A、B兩塊石頭捆在一起,據此進行推導:
如果p成立。因A+B比A重,那么,A+B的下落速度比A快(用q表示);
如果p成立,因速度小的B加在速度大的A上會減低A的速度,
那么,A+B的下落速度比A慢(這就是非q);
所以,p不成立。(即“物體下落速度與重量成正比”這一理論是錯誤的) 。

