算法簡介
(1)假設有K路數據流，流內部是有序的，且流間同為升序或降序；
(2)首先讀取每個流的第一個數，如果已經EOF，pass；
(3)將有效的k(k可能小於K)個數比較，選出最小的那路mink，輸出，讀取mink的下一個；
(4)直到所有K路都EOF。
多路歸併
方法一：循環遍歷
首先，我們比較所有k個數組的頭一個元素，找到最小的那一個，然後取出來。我們在該最小元素所在的數組取下一個元素，然後重複前面的過程去找最小的那個。這樣依次循環直到找到所有的元素。
代碼如圖：
循環遍歷用一個notEmpty來標誌所有序列是否已經遍歷完了。每次遍歷所有序列的當前元素，找到最小的。這樣每次找一個元素都要比較k次，假設所有n個元素，其總體時間複雜度就達到了O(nk)。
方法二：最小堆K路歸併排序
首先從k路序列中都取一個元素出來。因為所有的都是已經按照從小到大排序的，不需要考慮其他的。每個序列里取出來的肯定是這個序列里最小的，在這些最小元素里找到全局最小的那個。針對這個序列後面是否還有元素的問題，可以通過以下兩種方法處理：
1. 假定在處理元素的過程中，某個序列的元素取光了。我們可以在開始的時候針對所有序列的最後都加一個表示無窮大的數值。這樣如果取完這個序列之後可以保證它後續肯定不會被選擇到。
多路歸併算法2. 我們將該元素用堆最後的元素替換，然後調整堆的屬性並將堆的大小減1。這樣我們這個大小為k的堆慢慢會變成k-1, k-2,1這些個長度的堆。一直到我們把這些堆里序列的元素處理完 。
方法三：勝者樹K路並歸排序
首先，勝者樹的形式如圖：
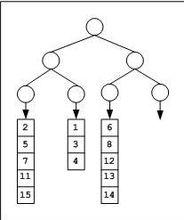勝者樹原始形式幾乎堆的每個葉節點對應一個輸入序列，將其構成一個完全二叉樹，進行一輪勝者的選擇之後，對結構如下：
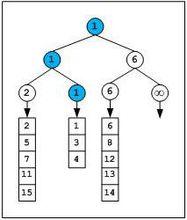一輪疊代之後的結構圖可以看出最終在堆頂的那個元素是最小的，而且有一條路徑從葉節點到堆的根。
通過在原來序列里取後續的元素，然後像勝者樹調整一樣向上，符合條件的元素放上面，然後一直比較到根。這樣就找到了下一個最小的元素。這樣一直循環下去。如果一個序列處理完了我們可以採用在末尾增加一個無窮大的值。
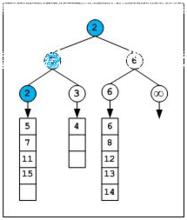勝者樹K路歸併圖總的來說，這個方法和普通的最小堆調整差不多，就是調整的方式不一樣而已 。
