頂點
n維正軸體的頂點有2n個,均為坐標形如(±1,0,0,…)的點。如二維正軸體(2-orthoplex)(即正方形)的4個頂點的坐標分別為(±1,0)、(0,±1);三維正軸體(3-orthoplex)((即正八面體)的6個頂點的坐標分別為(±1,0,0)、(0,±1,0)、(0,0,±1);四維正軸體(4-orthoplex)((即正十六胞體)的8個頂點的坐標分別為(±1,0,0,0)、(0,±1,0,0)、(0,0,±1,0)、(0,0,0,±1)。
表面
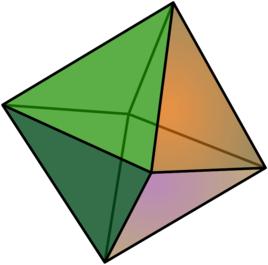
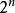 正軸體
正軸體 正軸體的表面由若干個單形(Simplex)組成,單形的個數為。如二維正軸體(2-orthoplex)(即正方形)的表面由4條線段組成;三維正軸體(3-orthoplex)((即正八面體)的表面由8個等邊三角形面組成;四維正軸體(4-orthoplex)((即正十六胞體)的表面由16個正五胞體組成。
計算
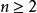 正軸體
正軸體 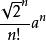 正軸體
正軸體 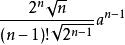 正軸體
正軸體 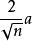 正軸體
正軸體 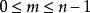 正軸體
正軸體 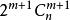 正軸體
正軸體 對於一個邊長為a的n維正軸體( ),其超體積為 ,其超表面積為 ,其對角線長為 ,其頂點個數為2n,其m( )維元素個數為 。
關係
連線一個n維正軸體表面各胞的中心,可得一個n維超立方體(n-cube)。對這個n維超立方體進行相同的操作也可以得到這個n為正軸體。
其他性質
n維正軸體的其他有關性質見下表:
| 維數 | 名稱 | 圖形 | 施萊夫利符號 | 點數 | 線數 | 面數 | 胞數 | 四維胞數 | 五維胞數 |
| 1 | 線段 |  1維正軸體 1維正軸體 |  正軸體 正軸體 | 2 | 1 | ||||
| 2 | 正方形 | 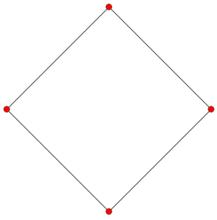 二維正軸體 二維正軸體 | 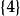 正軸體 正軸體  正軸體 正軸體 | 4 | 4 | 1 | |||
| 3 | 正八面體 | 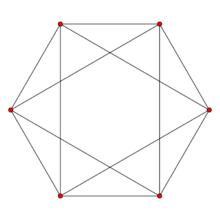 3維正軸體 3維正軸體 | 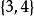 正軸體 正軸體 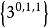 正軸體 正軸體 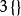 正軸體 正軸體 | 6 | 12 | 8 | 1 | ||
| 4 | 正十六胞體 | 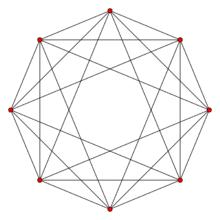 4維正軸體 4維正軸體 | 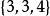 正軸體 正軸體 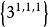 正軸體 正軸體 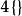 正軸體 正軸體 | 8 | 24 | 32 | 16 | 1 | |
| 5 | 五維正軸體 | 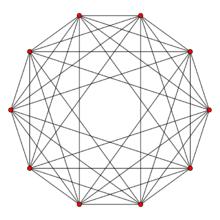 5維正軸體 5維正軸體 | 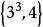 正軸體 正軸體 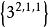 正軸體 正軸體 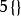 正軸體 正軸體 | 10 | 40 | 80 | 80 | 32 | 1 |
| 6 | 六維正軸體 | 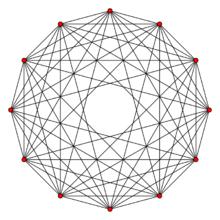 6維正軸形 6維正軸形 | 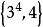 正軸體 正軸體 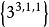 正軸體 正軸體 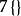 正軸體 正軸體 | 12 | 60 | 160 | 240 | 192 | 64 |
| n | n維正軸體 | 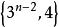 正軸體 正軸體 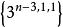 正軸體 正軸體  正軸體 正軸體 | 2n | 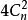 正軸體 正軸體 | 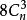 正軸體 正軸體 | 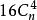 正軸體 正軸體 | 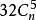 正軸體 正軸體 | 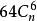 正軸體 正軸體 |