基本介紹
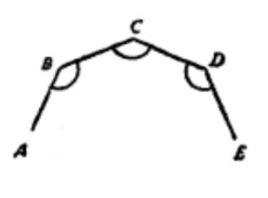
符合下面三個條件的折線叫做 正折線。
(1)組成折線的各線段(折線的邊)都相等;
(2)各相鄰兩邊所夾得角相等;
(3)各相鄰三邊中,第一邊和第三邊在第二邊的同一側。
例如上圖中的ABCDE和FGHKL都是正折線,但是MNPQR就不是正折線,因為它雖然符合第一個第二個條件,可是它不符合第三個條件,所以不能叫正折線,雖然這樣,可是ABCDE和FGHKL中間還有區別,怎樣區別呢?ABCDE不但是正折線,並且也是凸折線,因為把任何一邊向雙方延長的時候,其它各邊都在這條直線的同旁,所以它應該叫做凸正折線,折線FGHKL卻只是正折線,而不是凸折線 。
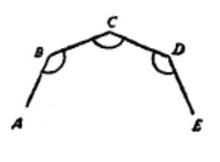 圖1 圖1 | 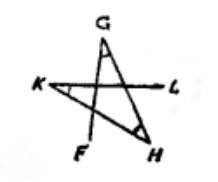 圖2 圖2 | 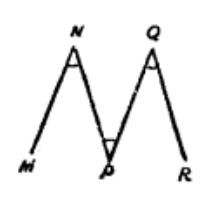 圖3 圖3 |
正折線與凸多邊形
凸多邊形的各邊相等且各角相等的,稱為正多邊形,折線的各邊相等且各角相等而有同一轉向的,稱為正折線。
定理 設將圓周分為n等分,則
1°分點是正多邊形的頂點;
2°圓周在這些點的切線是另一個正多邊形的邊。
1°在以各分點作頂點的多邊形中,顯然相鄰的兩邊對稱於通過其公共頂點的半徑;相鄰的兩角對稱於與其公共邊垂直的半徑。
2°在各分點的切線所形成的多邊形中,顯然相鄰的兩角對稱於與其公共邊垂直的半徑;相鄰的兩邊對稱於與聯結切點的弦成垂直的半徑。
逆定理 任一正多邊形,或者更普遍些,任一正折線,可以內接於一圓周,且外切於另一圓周 。
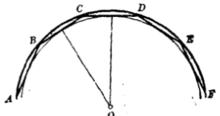 圖4
圖4例如設ABCDEF(圖4)為正折線,作三角形ABC的外接圓周;它的圓心O線上段BC的中垂線上,則這圓周也通過點D,要證明這個,只要注意兩邊AB及CD對稱於BC的中垂線,因為與BA對稱的線段,其方向(由於B, C兩角相等)和大小(因BA=CD)都與CD的相同,因之OA=OD。仿此可知,三角形BCD的外接圓周(即是方才的圓周)也通過點E,以下類推。
並且AB,BC等等既是新作圓周的等弦,就和它的圓心相距等遠;所以已知折線外切於另一個以O為圓心的圓周。
這第二圓的半徑,就是每一邊到圓心的距離,稱為這 正折線(或正多邊形) 的邊心距。
備註 任一正n邊形可用旋轉(即旋轉角以圓周n分之一的整數倍度量的那些旋轉)和對稱(關於各邊中垂線的對稱,以及關於各角平分線的對稱)以重迭於自身 。
正折線與球面的面積
把半圓上的一條弧(如圖5中的AD或BE)以半圓的直徑AF為軸旋轉一周所得的球冠或球帶的面積規定為:這一條弧內的內接正折線以同一直徑為軸旋轉一周所得的面,當這正折線的邊數無限增加時,它的面積的極限。
這個定義也包括了球面的面積的定義,對於球面來說,內接正折線是在整個半圓內的 。
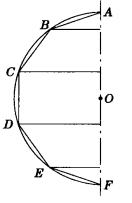 圖5
圖5